научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 8, август 2008
УДК 519.6
Карпенко А.П.
(д.ф.-м.наук, профессор МГТУ им.Н.Э.Баумана,
телефон: 263-65-26, E-mail: karpenko@nog.ru)
Федорук В.Г.
(к.т.н., доцент МГТУ им.Н.Э.Баумана,
телефон: 263-65-26, E-mail: fedoruk@comcor.ru)
Работа является четвертой в серии работ, посвященных адаптивным методам решения непрерывной конечномерной задачи многокритериальной оптимизации. В работах [1-3] рассмотрены методы аппроксимации функции предпочтений лица, принимающего решения (ЛПР), на основе планов первого и второго порядков, а также нейронных сетей и нечеткой логики. Данная работа посвящена рассмотрению адаптивных методов решения задачи многокритериальной оптимизации, построенных на базе указанных методов аппроксимации.
1. Основные обозначения и общая схема методов
Постановка задачи многокритериальной оптимизации приведена в работе [1]. Повторим основные обозначения, введенные там.
Вектор ![]() - n-мерный вектор параметров задачи (вектор варьируемых параметров), где
- n-мерный вектор параметров задачи (вектор варьируемых параметров), где
![]() -
-
замкнутое множество допустимых значений вектора параметров, ![]() - ограничивающие функции.
- ограничивающие функции.
![]() - векторный критерий оптимальности, определенный на множестве
- векторный критерий оптимальности, определенный на множестве ![]() . ЛПР стремится минимизировать каждый из частных критериев
. ЛПР стремится минимизировать каждый из частных критериев ![]() .
.
Полагается, что все частные критерии тем или иным способом нормализованы и за нормализованными частными критериями оптимальности сохранены обозначения ![]() .
.
Решение задачи многокритериальной оптимизации отыскивается с помощью метода скалярной сверки, который при каждом фиксированном векторе ![]() сводит решение этой задачи к решению однокритериальной задачи глобальной условной оптимизации
сводит решение этой задачи к решению однокритериальной задачи глобальной условной оптимизации
![]() , (1)
, (1)
где ![]() - результат операции свертки (суперкритерий),
- результат операции свертки (суперкритерий),
![]()
![]() -
-
вектор весовых множителей, ![]() - множество допустимых значений этого вектора.
- множество допустимых значений этого вектора.
Если при каждом ![]() решение задачи (1) единственно, то условие (1) ставит в соответствие каждому из допустимых векторов
решение задачи (1) единственно, то условие (1) ставит в соответствие каждому из допустимых векторов ![]() единственный вектор
единственный вектор ![]() и соответствующие значения частных критериев оптимальности
и соответствующие значения частных критериев оптимальности ![]() . Это обстоятельство позволяет полагать, что функция предпочтения ЛПР
. Это обстоятельство позволяет полагать, что функция предпочтения ЛПР ![]() определена не на множестве
определена не на множестве ![]() , а на множестве
, а на множестве ![]() :
:
![]() .
.
В результате задача многокритериальной оптимизации сводится к задаче выбора вектора ![]() такого, что
такого, что
![]() . (2)
. (2)
Величина ![]() полагается лингвистической переменной со значениями ”Очень-очень плохо”, ”Очень плохо”, …, ”Отлично”. Центры соответствующих нечетких множеств обозначаются
полагается лингвистической переменной со значениями ”Очень-очень плохо”, ”Очень плохо”, …, ”Отлично”. Центры соответствующих нечетких множеств обозначаются ![]() и имеют значения 1, 2, …, 9, соответственно.
и имеют значения 1, 2, …, 9, соответственно.
Используется также сведение задачи многокритериальной оптимизации к задаче отыскания вектора ![]() , обеспечивающего максимальное значение четкой дискретной функции
, обеспечивающего максимальное значение четкой дискретной функции ![]() :
:
![]() . (3)
. (3)
Общая схема предлагаемых методов состоит из следующих основных этапов:
1) задание ЛПР начальной точки ![]() ,
, ![]() ;
;
2) выполнение на основе планов первого порядка серии экстремальных экспериментов по максимизации функции предпочтений ![]() ;
;
3) построение по результатам указанных экспериментов первой аппроксимирующей функции ![]() ;
;
4) формирование области планирования для аппроксимации функции ![]() ;
;
5) построение второй аппроксимирующей функции ![]() ;
;
6) определение начальной точки ![]() для следующей итерации.
для следующей итерации.
На этапе 2 используются симплекс-планы на основе правильных или неправильных симплексов, а также регрессионные планы первого порядка [1]; на этапе 3 – аппроксимация кусочно-линейной функцией [1], персептронной нейронной сетью и нейронной сетью с радиальными базисными функциями [3], а также аппроксимация на основе нечетких множеств [3]; на этапах 5, 6 – линейная и квадратичная аппроксимация [2].
2. Этап 2 – экстремальный эксперимент на основе планов первого порядка
В данном разделе рассматриваются экстремальные эксперименты по максимизации функции ![]() на основе симплекс-планов, а также регрессионных планов первого порядка [1]. В подразделе 2.1 рассматривается экстремальный эксперимент на основе правильных симплексов, в подразделе 2.2 – на основе неправильных симплексов, в подразделе 2.3 – экстремальный эксперимент на основе регрессионных планов первого порядка и градиентного метода оптимизации с дроблением шага, в подразделе 2.4 – такой же эксперимент, но основе градиентного метода крутого восхождения [4].
на основе симплекс-планов, а также регрессионных планов первого порядка [1]. В подразделе 2.1 рассматривается экстремальный эксперимент на основе правильных симплексов, в подразделе 2.2 – на основе неправильных симплексов, в подразделе 2.3 – экстремальный эксперимент на основе регрессионных планов первого порядка и градиентного метода оптимизации с дроблением шага, в подразделе 2.4 – такой же эксперимент, но основе градиентного метода крутого восхождения [4].
2.1 Правильные симплекс-планы (метод М2.1). Отметим прежде, что по количеству точек в спектре симплекс-планы являются насыщенными планам, т.е. требуют минимально возможного количества испытаний, однако имеют низкую помехозащищенность (сглаживание отсутствует) [4].
Экстремальный эксперимент выполняется по следующей схеме (здесь и далее приводятся упрощенные схемы) [1].
1) Исходя из текущей начальной точки ![]() , СМКО (Система МногоКритериальной Оптимизации - Multi Criteria Decision Making System) строит начальный правильный симплекс
, СМКО (Система МногоКритериальной Оптимизации - Multi Criteria Decision Making System) строит начальный правильный симплекс ![]() , где
, где ![]() . Если одна или несколько вершин симплекса оказываются вне области допустимых значений
. Если одна или несколько вершин симплекса оказываются вне области допустимых значений ![]() , то СМКО выдает ЛПР соответствующее сообщение и предлагает либо изменить начальную точку
, то СМКО выдает ЛПР соответствующее сообщение и предлагает либо изменить начальную точку ![]() , либо уменьшить текущую длину ребра симплекса
, либо уменьшить текущую длину ребра симплекса ![]() .
.
2) Для каждой из вершин ![]() ,
, ![]() симплекса
симплекса ![]() СМКО выполняет следующие действия.
СМКО выполняет следующие действия.
2.1) Решает задачу (1) с весами ![]() .
.
2.2) Полученные значения компонентов вектора параметров ![]() , а также соответствующие значения частных критериев оптимальности
, а также соответствующие значения частных критериев оптимальности ![]() предъявляет ЛПР.
предъявляет ЛПР.
2.3) Запрашивает у ЛПР оценку предъявленного решения задачи многокритериальной оптимизации - требует ввести соответствующее значение лингвистической переменной ![]() .
.
3) СМКО находит минимальное и максимальное значения соответствующих четких значений лингвистической переменной
![]()
![]()
![]() ,
, ![]()
![]() .
.
4) По приведенной ниже схеме СМКО отражает вершину ![]() симплекса
симплекса ![]() относительно центра тяжести оставшихся вершин
относительно центра тяжести оставшихся вершин ![]() - находит вершину
- находит вершину ![]() и новый симплекс
и новый симплекс ![]() .
.
4.1) Если имеется несколько вершин симплекса ![]() , в которых величина
, в которых величина ![]() принимает одно и то же значение
принимает одно и то же значение ![]() , то отражаемая вершина выбирается случайным образом.
, то отражаемая вершина выбирается случайным образом.
4.2) Если отраженная вершина недопустима, то делается попытка отразить другую вершину, выбранную также случайным образом.
4.3) Если отражение всех указанных вершин не привело к успеху, то аналогично делается попытка отразить вершины, в которых величина ![]() имеет следующее за
имеет следующее за ![]() значение, и т.д. до вершин, в которых величина
значение, и т.д. до вершин, в которых величина ![]() имеет значение
имеет значение ![]() .
.
4.4) Если имеет место вращение симплекса вокруг некоторой его вершины, то СМКО информирует об этом пользователя и предлагает (а) закончить вычисления, (б) уменьшить текущую длину ребра симплекса ![]() и/или начать новый поиск из новой начальной точки.
и/или начать новый поиск из новой начальной точки.
4.5) Если ЛПР выбирает вариант (а), то СМКО формирует для ЛПР соответствующее сообщение и завершает вычисления. Если выбирается вариант (б), то СМКО полагает ![]() и выполняет переход к п. 1 (здесь
и выполняет переход к п. 1 (здесь ![]() - свободный параметр метода).
- свободный параметр метода).
5) Для вершины ![]() СМКО выполняет действия, аналогичные действиям, указанным в п.2 (в результате становится известной величина
СМКО выполняет действия, аналогичные действиям, указанным в п.2 (в результате становится известной величина ![]() ), полагает
), полагает ![]() и переходит к п.3.
и переходит к п.3.
Заметим, что в этой схеме на всех итерациях, кроме первой, от ЛПР требуется оценка только одного решения.
2.2 Неправильные симплекс-планы (метод М2.2). Эксперимент выполняется по упрощенной схеме метода Нелдера-Мида [5]. Упрощение заключается в исключении из числа операций над симплексом операции редукции (поскольку эта операция требует от ЛПР оценки значений функции предпочтений в ![]() точках, в отличие от одной точки для операций отражения, сжатия и растяжения симплекса). Эксперимент выполняется по следующей схеме [1].
точках, в отличие от одной точки для операций отражения, сжатия и растяжения симплекса). Эксперимент выполняется по следующей схеме [1].
1) Исходя из текущей начальной точки ![]() ,
, ![]() СМКО строит начальный правильный симплекс
СМКО строит начальный правильный симплекс ![]() (см. подраздел 2.1).
(см. подраздел 2.1).
2) Для каждой из вершин ![]() симплекса
симплекса ![]() СМКО решает задачу (1) и получает от ЛПР соответствующее значение лингвистической переменной
СМКО решает задачу (1) и получает от ЛПР соответствующее значение лингвистической переменной ![]() (см. подраздел 2.1).
(см. подраздел 2.1).
3) СМКО находит минимальное, максимальное, а также первое, предшествующее максимальному, значения соответствующих четких значений
![]()
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() .
.
4) СМКО отражает вершину ![]() симплекса
симплекса ![]() относительно центра тяжести оставшихся вершин
относительно центра тяжести оставшихся вершин ![]() - находит вершину
- находит вершину ![]() и новый симплекс
и новый симплекс ![]() . СМКО запрашивает у ЛПР оценку
. СМКО запрашивает у ЛПР оценку ![]() решения, соответствующего точке
решения, соответствующего точке ![]() (см. подраздел 2.1). Если
(см. подраздел 2.1). Если ![]() и
и ![]() , то выполняется переход к п.5. Если
, то выполняется переход к п.5. Если ![]() , но
, но ![]() , то выполняется переход к п.4, а если
, то выполняется переход к п.4, а если ![]() - к п.6.
- к п.6.
5) СМКО выполняет растяжение симплекса ![]() в направлении
в направлении ![]() - находит новый симплекс
- находит новый симплекс ![]() и запрашивает у ЛПР оценку
и запрашивает у ЛПР оценку ![]() . Если
. Если ![]() , то выполняется переход к операции отражения симплекса
, то выполняется переход к операции отражения симплекса ![]() (п.4), иначе – к операции отражения симплекса
(п.4), иначе – к операции отражения симплекса ![]() (п.4).
(п.4).
6) СМКО выполняет сжатие симплекса ![]() в направлении
в направлении ![]() - находит новый симплекс
- находит новый симплекс ![]() . МСКО запрашивает у ЛПР оценку
. МСКО запрашивает у ЛПР оценку ![]() и выполняет переход к операции отражения симплекса
и выполняет переход к операции отражения симплекса ![]() .
.
2.3. Регрессионные планы первого порядка и градиентный метод с дроблением шага (метод М2.3). Для исходных («натуральных») факторов ![]() искомая линейная регрессионная модель имеет вид
искомая линейная регрессионная модель имеет вид
![]() ,
,
где ![]() - неизвестные коэффициенты регрессии [4]. Переход от исходных факторов
- неизвестные коэффициенты регрессии [4]. Переход от исходных факторов ![]() к нормированным (стандартным) факторам
к нормированным (стандартным) факторам ![]() выполняется по формуле
выполняется по формуле ![]() ,
, ![]() ,
, ![]() , где
, где ![]() - основной (базовый) уровень фактора
- основной (базовый) уровень фактора ![]() , а
, а ![]() - шаг варьирования этого фактора. Для нормированных факторов искомая регрессионная модель имеет вид
- шаг варьирования этого фактора. Для нормированных факторов искомая регрессионная модель имеет вид
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() .
.
Экстремальный эксперимент в данном случае строится на основе слабо не насыщенных регрессионных планов первого порядка для количества критериев ![]() . Планы объединены в библиотеку планов
. Планы объединены в библиотеку планов ![]() , основные параметры которой представлены в Табл. 1. Здесь M – требуемое количество опытов,
, основные параметры которой представлены в Табл. 1. Здесь M – требуемое количество опытов, ![]() - число степеней свободы, ПФЭ – полный факторный эксперимент, ДФЭ – дробный факторный эксперимент. Как это принято при планировании экспериментов, планы в библиотеки даны не для «натуральных», а для нормированных факторов [4].
- число степеней свободы, ПФЭ – полный факторный эксперимент, ДФЭ – дробный факторный эксперимент. Как это принято при планировании экспериментов, планы в библиотеки даны не для «натуральных», а для нормированных факторов [4].
С точки зрения помехозащищенности наиболее эффективными являются планы ПФЭ ![]() . Однако эти планы требуют большого количества испытаний. Поэтому при разработке указанной библиотеки планов в работе принято компромиссное решение – там, где это возможно, используются планы ДФЭ
. Однако эти планы требуют большого количества испытаний. Поэтому при разработке указанной библиотеки планов в работе принято компромиссное решение – там, где это возможно, используются планы ДФЭ ![]() ,
, ![]() .
.
Таблица 1. Основные параметры библиотечных планов первого порядка
|
╧ п.п. |
m |
План |
M |
|
|
1 |
2 |
ПФЭ |
4 |
1 |
|
2 |
3 |
ПФЭ |
8 |
4 |
|
3 |
3 |
ДФЭ |
4 |
0 |
|
4 |
4 |
ДФЭ |
8 |
3 |
|
5 |
5 |
ДФЭ |
16 |
10 |
|
6 |
5 |
ДФЭ |
8 |
2 |
|
7 |
6 |
ДФЭ |
16 |
9 |
|
8 |
6 |
ДФЭ |
8 |
1 |
|
9 |
7 |
ДФЭ |
16 |
8 |
|
10 |
7 |
ДФЭ |
8 |
0 |
|
11 |
8 |
ДФЭ |
16 |
7 |
|
12 |
9 |
ДФЭ |
32 |
22 |
|
13 |
9 |
ДФЭ |
16 |
6 |
|
14 |
10 |
ДФЭ |
32 |
21 |
|
15 |
10 |
ДФЭ |
16 |
5 |
Схема эксперимента на основе регрессионных планов первого порядка и градиентного метода с дроблением шага имеет следующий вид.
1) Исходя из текущей начальной точки ![]() , СМКО строит область планирования в виде параллелепипеда
, СМКО строит область планирования в виде параллелепипеда ![]()
![]() ,
, ![]() ). Здесь
). Здесь ![]() - шаг варьирования фактора
- шаг варьирования фактора ![]() на r-ой итерации.
на r-ой итерации.
2) СМКО выбирает из библиотеки планов соответствующий план первого порядка ![]() ,
, ![]() , выполняет переход от стандартных факторов
, выполняет переход от стандартных факторов ![]() к «натуральным» факторам
к «натуральным» факторам ![]() ,
, ![]() и проверяет принадлежность каждой из полученных точек области допустимых значений
и проверяет принадлежность каждой из полученных точек области допустимых значений ![]() . Если одна или несколько точек плана
. Если одна или несколько точек плана ![]() ,
, ![]() оказываются вне области допустимых значений
оказываются вне области допустимых значений ![]() , то СМКО выдает ЛПР соответствующее сообщение и предлагает либо изменить начальную точку
, то СМКО выдает ЛПР соответствующее сообщение и предлагает либо изменить начальную точку ![]() , либо уменьшить величины
, либо уменьшить величины ![]() .
.
3) Для каждой из точек плана ![]() ,
, ![]() СМКО выполняет следующие действия.
СМКО выполняет следующие действия.
3.1) Решает задачу (1) с весами ![]() . Полученные значения компонентов вектора параметров
. Полученные значения компонентов вектора параметров ![]() , а также соответствующие значения частных критериев оптимальности предъявляет ЛПР.
, а также соответствующие значения частных критериев оптимальности предъявляет ЛПР.
3.2) Запрашивает у ЛПР оценку каждого из предъявленных решений - требует ввести соответствующее значение лингвистической переменной ![]() .
.
4) Для каждой из точек плана ![]() ,
, ![]() СМКО формирует
СМКО формирует ![]() значений базисных функций
значений базисных функций
![]() ,
,
в результате чего становится известной ![]() -матрица
-матрица
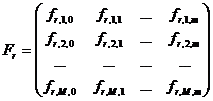 .
.
5) СМКО решает систему линейных алгебраических уравнений (СЛАУ)
![]() , (4)
, (4)
где симметричная ![]() матрица
матрица ![]() есть информационная матрица (Фишера),
есть информационная матрица (Фишера), ![]() - вектор соответствующих четких значений лингвистической переменной
- вектор соответствующих четких значений лингвистической переменной ![]() ,
, ![]() - вектор оценок коэффициентов регрессии для стандартных факторов. Поскольку для всех библиотечных планов матрица Фишера
- вектор оценок коэффициентов регрессии для стандартных факторов. Поскольку для всех библиотечных планов матрица Фишера ![]() является диагональной с диагональными элементами, равными количеству опытов
является диагональной с диагональными элементами, равными количеству опытов ![]() , решение СЛАУ (4) не представляет труда.
, решение СЛАУ (4) не представляет труда.
6) СМКО выполняет следующие действия [4]:
6.1) Осуществляет проверку значимости оценок коэффициентов регрессии ![]() ;
;
6.2) Вычисляет коэффициент детерминации ![]() и если
и если ![]() , где
, где ![]() , то выполняет переход к п. 7. Если
, то выполняет переход к п. 7. Если ![]() , то система предъявляет ЛПР величину
, то система предъявляет ЛПР величину ![]() и требует его разрешения продолжить итерации. При ответе «Да» выполняется переход к следующему пункту, а при ответе «Нет» - вычисления заканчиваются.
и требует его разрешения продолжить итерации. При ответе «Да» выполняется переход к следующему пункту, а при ответе «Нет» - вычисления заканчиваются.
7) СМКО вычисляет градиент построенной функции регрессии и делает шаг в его направлении по следующей схеме:
7.1) Определяет компоненты ![]() вектора
вектора ![]() для натуральных факторов по формуле
для натуральных факторов по формуле 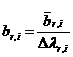 ,
, ![]() .
.
7.2) Вычисляет текущую величину шага ![]() в направлении градиента, где
в направлении градиента, где ![]() - свободный параметр метода, а величина
- свободный параметр метода, а величина ![]() выбирается из условия
выбирается из условия ![]() =
=![]() .
.
7.3) Вычисляет координаты нового центра серии опытов
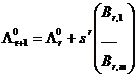 , где
, где 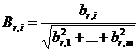 -
-
нормированные компоненты вектора градиента для натуральных факторов.
7.4) Проверяет допустимость точки ![]() . Если точка недопустима, то а) уменьшает длину текущего шага
. Если точка недопустима, то а) уменьшает длину текущего шага ![]() , т.е. полагает
, т.е. полагает ![]() , где
, где ![]() - свободный параметр алгоритма; б) выполняет переход к п. 7.3. Если точка допустима, то полагает
- свободный параметр алгоритма; б) выполняет переход к п. 7.3. Если точка допустима, то полагает ![]() и переходит к п.1.
и переходит к п.1.
2.4. Регрессионные планы первого порядка и градиентный метод крутого восхождения (метод М2.4). Схема эксперимента в этом случае аналогична схеме, рассмотренной в подразделе 2.3. Отличия имеются лишь в пункте 7, который рассматривается ниже.
7) СМКО вычисляет градиент построенной функции регрессии и делает шаг в его направлении по следующей схеме.
………….
7.5) Проверяет допустимость точки ![]() . Если точка недопустима, то уменьшает длину текущего шага
. Если точка недопустима, то уменьшает длину текущего шага ![]() и выполняет переход к п. 7.3. Если точка допустима, то выполняет следующие действия.
и выполняет переход к п. 7.3. Если точка допустима, то выполняет следующие действия.
7.5.1) Решает задачу (1) с весами ![]() . Полученный в результате вектор параметров
. Полученный в результате вектор параметров ![]() , а также соответствующие значения частных критериев оптимальности предъявляет ЛПР. Запрашивает у ЛПР оценку предъявленного решения - требует ввести соответствующее значение лингвистической переменной
, а также соответствующие значения частных критериев оптимальности предъявляет ЛПР. Запрашивает у ЛПР оценку предъявленного решения - требует ввести соответствующее значение лингвистической переменной ![]() .
.
7.5.2) Если ![]() , то на основе диалога с ЛПР либо завершает вычисления, либо уменьшает шаги варьирования факторов
, то на основе диалога с ЛПР либо завершает вычисления, либо уменьшает шаги варьирования факторов ![]() ,
, ![]() , полагает
, полагает ![]() и переходит к п.1. Ситуация интерпретируется как достижение максимума функции предпочтений в направлении градиента.
и переходит к п.1. Ситуация интерпретируется как достижение максимума функции предпочтений в направлении градиента.
7.5.3) Если ![]() , то полагает,
, то полагает, ![]() ,
, ![]() и переходит к п.7.3. Ситуация интерпретируется следующим образом: в направлении градиента максимум функции предпочтений не достигнут и можно сделать еще один шаг в том же направлении.
и переходит к п.7.3. Ситуация интерпретируется следующим образом: в направлении градиента максимум функции предпочтений не достигнут и можно сделать еще один шаг в том же направлении.
3. Этап 3 - построение вспомогательной аппроксимирующей функции
В данном разделе рассматривается построение первой (вспомогательной) аппроксимирующей функции ![]() на основе результатов серии экстремальных экспериментов, рассмотренных в предыдущем разделе. В подразделе 3.1 рассматривается кусочно-линейная аппроксимация на основе правильных симплекс-планов [1]; в подразделе 3.2- на основе неправильных симплекс-планов; в подразделе 3.3 - кусочно-линейная аппроксимация на основе регрессионных планов первого порядка [1]; в подразделе 3.4 - аппроксимация многослойной персептронной нейронной сетью (MLP-нейронной сетью) [3]; в подразделе 3.5 - аппроксимация нейронной сетью на основе радиальных базисных функций (RBF-нейронной сетью) [3]; в подразделе 3.6 - аппроксимация на основе теории нечетких множеств [3].
на основе результатов серии экстремальных экспериментов, рассмотренных в предыдущем разделе. В подразделе 3.1 рассматривается кусочно-линейная аппроксимация на основе правильных симплекс-планов [1]; в подразделе 3.2- на основе неправильных симплекс-планов; в подразделе 3.3 - кусочно-линейная аппроксимация на основе регрессионных планов первого порядка [1]; в подразделе 3.4 - аппроксимация многослойной персептронной нейронной сетью (MLP-нейронной сетью) [3]; в подразделе 3.5 - аппроксимация нейронной сетью на основе радиальных базисных функций (RBF-нейронной сетью) [3]; в подразделе 3.6 - аппроксимация на основе теории нечетких множеств [3].
3.1. Кусочно-линейная аппроксимация на основе правильных симплекс-планов (метод М3.1) [1]. Пусть по схеме, приведенной в подразделе 2.1, последовательно построены правильные симплексы ![]() ,
, ![]() ,…,
,…,![]() . Тогда построение кусочно-линейной аппроксимации
. Тогда построение кусочно-линейной аппроксимации ![]() функции предпочтений ЛПР выполняется по следующей схеме (см. Рис. 1).
функции предпочтений ЛПР выполняется по следующей схеме (см. Рис. 1).
1) СМКО строит линейные функции ![]() ,
, ![]() ,…,
,…,![]() , имеющие в вершинах соответствующих симплексов значения
, имеющие в вершинах соответствующих симплексов значения ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() , а также гиперплоскости
, а также гиперплоскости ![]() ,
, ![]() ,…,
,…,![]() , проходящие через общие точки смежных симплексов.
, проходящие через общие точки смежных симплексов.
2) СМКО строит кусочно-линейную аппроксимирующую функцию
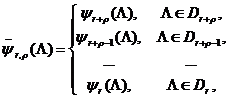 (5)
(5)
где
![]() ,
,
![]() ,
,
…
![]() .
.
Здесь ![]() - центр тяжести симплекса
- центр тяжести симплекса ![]() ,
, ![]() . Заметим, что вместо центра тяжести симплекса
. Заметим, что вместо центра тяжести симплекса ![]() более удобным может быть использование той из его вершин, которая лежит вне гиперплоскости
более удобным может быть использование той из его вершин, которая лежит вне гиперплоскости ![]() .
.
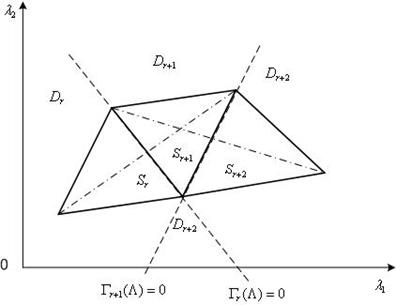
Рис. 1. К кусочно-линейной аппроксимации функции предпочтений ЛПР на симплексах: ![]() ;
; ![]() .
.
Заметим, что приведенная схема аппроксимации учитывает тот факт, что с ростом количества итераций ЛПР обычно оценивает свою функцию предпочтений более точно.
Поясним первый пункт приведенной схемы. Рассмотрим для примера построение линейной функции ![]() , где
, где ![]() ,
, ![]() ,
, ![]() - искомые коэффициенты. Из условия прохождения функции
- искомые коэффициенты. Из условия прохождения функции ![]() через точки
через точки ![]() , имеем следующую СЛАУ для определения этих коэффициентов:
, имеем следующую СЛАУ для определения этих коэффициентов:
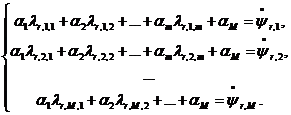 (6)
(6)
Таким образом, построение функций ![]() ,
, ![]() ,…,
,…, ![]() сводится к решению СЛАУ вида (6). Поскольку все точки
сводится к решению СЛАУ вида (6). Поскольку все точки ![]() ,
, ![]() различны, матрица этой системы не вырождена и решение существует и единственно.
различны, матрица этой системы не вырождена и решение существует и единственно.
Рассмотрим также для примера построение гиперплоскости ![]() . Положим, что симплекс
. Положим, что симплекс ![]() получен в результате отражения вершины
получен в результате отражения вершины ![]() симплекса
симплекса ![]() . Тогда общими для симплексов
. Тогда общими для симплексов ![]() ,
, ![]() являются m вершин
являются m вершин ![]() ,
, ![]() ,
, ![]() и линейную функцию
и линейную функцию ![]() можно записать в виде
можно записать в виде
![]()
![]() ,
,
где ![]() ,
, ![]() - искомые коэффициенты. Здесь аналогично предыдущему коэффициенты
- искомые коэффициенты. Здесь аналогично предыдущему коэффициенты ![]() определяются из СЛАУ
определяются из СЛАУ
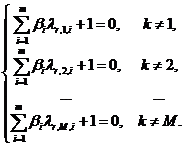
Матрица этой системы не вырождена и ее решение существует и единственно.
3.2. Кусочно-линейная аппроксимация на основе неправильных симплексов (метод М3.2) [1]. Аппроксимация на основе неправильных симплекс-планов выполняется по схеме п. 3. 1.
3.3. Кусочно-линейная аппроксимация на основе регрессионных планов первого порядка (метод М3.3) [1]. Пусть по схеме, приведенной в подразделе 2.3, последовательно построены области планирования в виде параллелепипедов ![]() ,
, ![]() ,…,
,…,![]() . Построение кусочно-линейной аппроксимирующей функции
. Построение кусочно-линейной аппроксимирующей функции ![]() в данном случае выполняется по следующей схеме (см. Рис. 2).
в данном случае выполняется по следующей схеме (см. Рис. 2).
1) СМКО строит гиперплоскости ![]() ,
, ![]() ,…,
,…,![]() такие, что в гиперплоскости
такие, что в гиперплоскости ![]() ,
, ![]() лежит та из граней параллелепипеда
лежит та из граней параллелепипеда![]() , которую пересекает отрезок прямой
, которую пересекает отрезок прямой ![]() .
.
2) В качестве искомой кусочно-линейной функции ![]() принимается функция (5), где
принимается функция (5), где ![]() ,
, ![]() ,…,
,…, ![]() - соответствующие линейные регрессионные модели,
- соответствующие линейные регрессионные модели,
![]() ,
,
![]() ,
,
…
![]() .
.
Как и в подразделе 3.1, приведенная схема аппроксимации учитывает тот факт, что с ростом количества итераций ЛПР обычно оценивает свою функцию предпочтений более точно.
Поясним первый пункт приведенной схемы. Рассмотрим для примера построение гиперплоскости ![]() .
.
а) Пронумеруем вершины параллелепипеда ![]() =
=![]() ,
, ![]() ) с помощью бинарного отраженного кода Грея. В результате любые две соседние вершины параллелепипеда
) с помощью бинарного отраженного кода Грея. В результате любые две соседние вершины параллелепипеда ![]() получат номера, двоичное представление которых имеет только одну различающуюся позицию [6].
получат номера, двоичное представление которых имеет только одну различающуюся позицию [6].
б) Пусть ![]() - ближайшая к точке
- ближайшая к точке ![]() вершина параллелепипеда
вершина параллелепипеда ![]() (найти ее легко путем перебора). Используя отмеченное выше свойство кода Грея, найдем все
(найти ее легко путем перебора). Используя отмеченное выше свойство кода Грея, найдем все ![]() вершин
вершин ![]() ,
, ![]() ,…,
,…, ![]() параллелепипеда
параллелепипеда ![]() , которые являются соседями вершины
, которые являются соседями вершины ![]() .
.
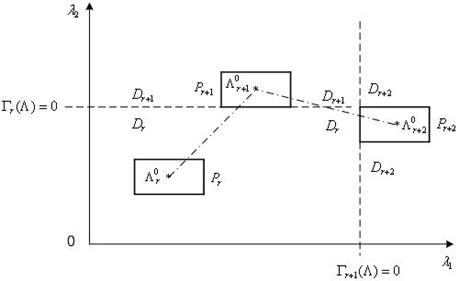
Рис. 2. К кусочно-линейной аппроксимации функции предпочтений ЛПР на параллелепипедах: ![]() ;
; ![]() .
.
в) Вершины ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() объединим в
объединим в ![]() различных совокупностей
различных совокупностей ![]()
![]() ,
, ![]()
![]() ….,
…., ![]() ,
, ![]() по
по ![]() вершин в каждой так, чтобы в каждую из этих совокупностей входила вершина
вершин в каждой так, чтобы в каждую из этих совокупностей входила вершина ![]() .
.
г) Из условия прохождения гиперплоскости ![]()
![]() через все вершины совокупности
через все вершины совокупности ![]() ,
, ![]() получим следующую СЛАУ для определения неизвестных коэффициентов
получим следующую СЛАУ для определения неизвестных коэффициентов ![]() ,
, ![]() :
:
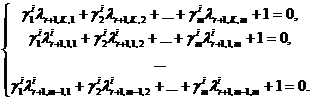
Матрица этой системы не вырождена и ее решение существует и единственно.
д) Найдем уравнение прямой, проходящей через точки ![]() ,
, ![]() :
:
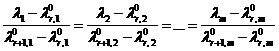 . (7)
. (7)
е) Из СЛАУ
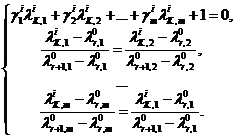
найдем точку ![]() пересечения прямой (7) с гиперплоскостью
пересечения прямой (7) с гиперплоскостью ![]() ,
, ![]() .
.
ж) Определим минимальное из расстояний от точки ![]() до точки
до точки ![]() :
:
![]() ,
, ![]() .
.
з) В качестве искомой гиперплоскости ![]() примем гиперплоскость
примем гиперплоскость ![]() .
.
3.4. Аппроксимация MLP-нейронной сетью (метод М3.4) [3]. Рассмотрим двухслойную MLP-сеть с сигмоидальными передаточными функциями, имеющую ![]() входных нейронов,
входных нейронов, ![]() нейронов в промежуточном слое и один выходной нейрон (см. Рис. 3). Обозначим выходы нейронов скрытого слоя
нейронов в промежуточном слое и один выходной нейрон (см. Рис. 3). Обозначим выходы нейронов скрытого слоя ![]() . Тогда при заданных весах
. Тогда при заданных весах ![]() ,
, ![]() ,
, ![]() ,
, ![]() и некоторых фиксированных
и некоторых фиксированных ![]() выход этой сети (значение искомой аппроксимирующей функции
выход этой сети (значение искомой аппроксимирующей функции ![]() ) определяется как суперпозиция функций
) определяется как суперпозиция функций
![]() ,
, 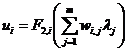 ,
, ![]() ,
,
где ![]() ,
, ![]() - передаточные функции нейронов
- передаточные функции нейронов ![]() ,
, ![]() , соответственно.
, соответственно.
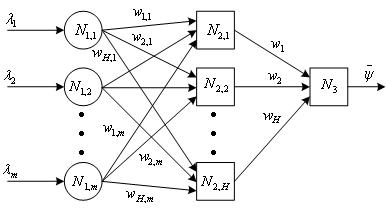
Рис. 3. Топология нейронной сети.
Пусть ![]() ,
, ![]() ,
, ![]() - совокупность различных точек множества
- совокупность различных точек множества ![]() , в которых ЛПР определены значения его функции предпочтений
, в которых ЛПР определены значения его функции предпочтений ![]() . При использовании симплекс-планов – это те из вершин симплексов
. При использовании симплекс-планов – это те из вершин симплексов ![]() ,
, ![]() ,…,
,…,![]() , формирование которых рассмотрено в подразделах 2.1, 2.2 и на основе которых в подразделе 3.1 построена аппроксимирующая функция
, формирование которых рассмотрено в подразделах 2.1, 2.2 и на основе которых в подразделе 3.1 построена аппроксимирующая функция ![]() . При использовании регрессионных планов первого порядка – это совокупность точек всех использованных планов (см. подразделы 2.3, 2.4). Заметим, что в случае использования симплекс-планов требование
. При использовании регрессионных планов первого порядка – это совокупность точек всех использованных планов (см. подразделы 2.3, 2.4). Заметим, что в случае использования симплекс-планов требование ![]() означает, что на этапе 2 должно быть построено минимум два симплекса
означает, что на этапе 2 должно быть построено минимум два симплекса ![]() ,
, ![]() , т.е.
, т.е. ![]()
![]() .
.
Построение аппроксимирующей функции ![]() с помощью MLP-нейронной сети выполняется по следующей схеме.
с помощью MLP-нейронной сети выполняется по следующей схеме.
1) СМКО строит двухслойную MLP-сеть с сигмоидальными передаточными функциями, имеющую ![]() входных нейронов,
входных нейронов, ![]() нейронов в промежуточном слое и один выходной нейрон (см. Рис. 3). Начальное количество нейронов
нейронов в промежуточном слое и один выходной нейрон (см. Рис. 3). Начальное количество нейронов ![]() определяется из равенства
определяется из равенства
![]() ,
,
где величина ![]() находится из условия
находится из условия
![]() .
.
2) На обучающей выборке ![]() ,
,![]() СМКО выполняет параметрический синтез нейронной сети – определяет веса
СМКО выполняет параметрический синтез нейронной сети – определяет веса ![]() ,
, ![]() ,
, ![]() ,
, ![]() . При этом в качестве оценки ошибки сети
. При этом в качестве оценки ошибки сети ![]() при обработке вектора
при обработке вектора ![]() используется величина
используется величина 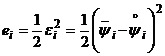 , а в качестве оценки ошибки при обработке всех N векторов из обучающей выборки - величина
, а в качестве оценки ошибки при обработке всех N векторов из обучающей выборки - величина 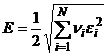 . Здесь
. Здесь ![]() - весовой множитель i-го примера из обучающей выборки, назначаемый по правилу экспоненциального возрастания весов опытов [3].
- весовой множитель i-го примера из обучающей выборки, назначаемый по правилу экспоненциального возрастания весов опытов [3].
3) Если заданная точность аппроксимации не достигнута, то методом динамического наращивания узлов [3] СМКО увеличивает количество узлов в скрытом слое и возвращается к п. 2.
3.5. Аппроксимация RBF-нейронной сетью (метод М3.5) [3]. Рассмотрим двухслойную RBF-сеть с сигмоидальными передаточными функциями в скрытом слое и линейной передаточной функцией ![]() в выходном слое (см. Рис. 3). Веса
в выходном слое (см. Рис. 3). Веса ![]() ,
, ![]() ,
, ![]() нейронов скрытого слоя положим равными единице, так что
нейронов скрытого слоя положим равными единице, так что ![]() . Тогда для некоторого входного вектора
. Тогда для некоторого входного вектора ![]() при заданных весах
при заданных весах ![]() ,
, ![]() выход этой сети, т.е. значение искомой аппроксимирующей функции, равен
выход этой сети, т.е. значение искомой аппроксимирующей функции, равен
![]()
![]() .
.
Аналогично п.3.4, в качестве обучающей выборки используем выборку ![]()
![]() , где
, где ![]() .
.
Построение аппроксимирующей функции ![]() с помощью RBF-нейронной сети выполняется по следующей схеме.
с помощью RBF-нейронной сети выполняется по следующей схеме.
1) Из выборки ![]()
![]() СМКО случайным образом формирует обучающие выборки
СМКО случайным образом формирует обучающие выборки ![]()
![]() . Здесь
. Здесь ![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
; ![]() - символ ближайшего целого большего.
- символ ближайшего целого большего.
2) СМКО строит двухслойную RBF-сеть, в которой каждому вектору ![]() из первой обучающей выборки ставится в соответствие нейрон скрытого слоя с центром в точке
из первой обучающей выборки ставится в соответствие нейрон скрытого слоя с центром в точке ![]() ,
, ![]() ,
, ![]() . Таким образом, передаточная функция
. Таким образом, передаточная функция 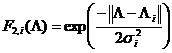 ,
, ![]() , где
, где ![]() - параметр, определяющий ширину колокола функции
- параметр, определяющий ширину колокола функции ![]() .
.
3) СМКО повторяет некоторое фиксированное количество раз ![]() следующие действия.
следующие действия.
3.1) Присваивает величинам ![]() ,
, ![]() некоторые положительные случайные начальные значения.
некоторые положительные случайные начальные значения.
3.2) Путем решения СЛАУ
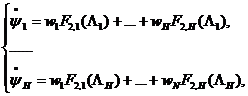
полученной на основе первой обучающей выборки, определяет веса ![]() выходного нейрона.
выходного нейрона.
3.3) С использованием второй обучающей выборки решает многомерную, вообще говоря, многоэкстремальную, задачу условной оптимизации
![]() ,
,
где функция ![]() , а
, а ![]() .
.
4) На основе результатов предыдущего пункта СМКО выбирает решение, обеспечивающее минимальное значения ошибки ![]() , а также соответствующие значения весов
, а также соответствующие значения весов ![]() .
.
3.6 Аппроксимация на основе нечетких множеств (метод М3.6) [3]. Пусть по схеме п. 3.5 построены обучающие выборки ![]()
![]()
![]() ,
, ![]() . Положим, что в рамках первой обучающей выборки
. Положим, что в рамках первой обучающей выборки ![]() раз переменная
раз переменная ![]() приняла значение
приняла значение ![]() ,
, ![]() раз - значение
раз - значение ![]() и т.д. до
и т.д. до ![]() и
и ![]() . Соответствующие входные векторы
. Соответствующие входные векторы ![]() обозначим
обозначим ![]() ,
, ![]() ,
, ![]() . Термы
. Термы ![]() и термы
и термы ![]() будем полагать нечеткими множествами, заданными на универсальном множестве
будем полагать нечеткими множествами, заданными на универсальном множестве ![]() :
:
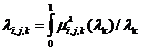 ,
, ![]() ;
;
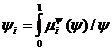 ,
, ![]() .
.
Здесь ![]() - функция принадлежности величины
- функция принадлежности величины ![]() терму
терму ![]() ,
, ![]() - функция принадлежности значений лингвистической переменной
- функция принадлежности значений лингвистической переменной ![]() терму
терму ![]() .
.
Во введенных обозначениях многомерная функция принадлежности ![]() имеет вид
имеет вид
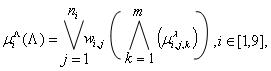
где ![]() - весовые множители, определяемые модифицированным правилом экспоненциального возрастания весов опытов -
- весовые множители, определяемые модифицированным правилом экспоненциального возрастания весов опытов - ![]() . Здесь
. Здесь ![]() - свободный параметр алгоритма, величина
- свободный параметр алгоритма, величина ![]() находится из условия
находится из условия ![]() , I – номер опыта по порядку [3],
, I – номер опыта по порядку [3], ![]() - малая положительная величина.
- малая положительная величина.
Обозначим ![]() ,b полуширины функций принадлежности
,b полуширины функций принадлежности ![]() ,
, ![]() , соответственно. Область допустимых значений параметров
, соответственно. Область допустимых значений параметров ![]() определим как
определим как ![]() =
=![]() ;
; ![]() ;
; ![]() , где
, где ![]() - заданные константы.
- заданные константы.
Построение аппроксимирующей функции ![]() с помощью нечетких множеств выполняется по следующей схеме.
с помощью нечетких множеств выполняется по следующей схеме.
1) С использованием операций объединения и пересечения множеств СМКО формирует базу знаний в виде совокупности логических высказываний
![]() ,
, ![]() .
.
2) СМКО осуществляет параметрическую оптимизацию построенной нечеткой модели – повторяет некоторое фиксированное количество раз ![]() следующие действия.
следующие действия.
2.1) Присваивает величинам ![]() некоторые допустимые случайные начальные значения.
некоторые допустимые случайные начальные значения.
2.2) Исходя из этих значений, решает на второй обучающей выборке ![]() задачу многомерной, вообще говоря, многоэкстремальной условной оптимизации
задачу многомерной, вообще говоря, многоэкстремальной условной оптимизации
![]() ,
,
где критерий оптимальности ![]() имеет вид
имеет вид
![]() ,
, ![]() .
.
Здесь значения аппроксимирующей функции ![]() определяются по следующей схеме.
определяются по следующей схеме.
2.2.1) Для данного вектора ![]() определяется значение многомерной функции принадлежности
определяется значение многомерной функции принадлежности ![]() .
.
2.2.2) Функцию принадлежности ![]() «срезается» на уровне
«срезается» на уровне ![]() ,
, ![]() .
.
2.2.3) Полученные нечеткие множества агрегируются – строится нечеткое множество
![]()
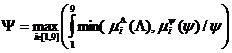
с функцией принадлежности ![]() .
.
2.2.4) Определяется четкое значение функции ![]() , соответствующее входному вектору
, соответствующее входному вектору ![]() - т.е. выполняет операцию дефаззификации нечеткого множества
- т.е. выполняет операцию дефаззификации нечеткого множества ![]() , например, по методу центра тяжести.
, например, по методу центра тяжести.
3) На основе результатов предыдущего пункта СМКО выбирает значения параметров ![]() , обеспечивающие минимальное значение ошибки
, обеспечивающие минимальное значение ошибки ![]() .
.
После построения по рассмотренной схеме аппроксимирующей функции ![]() ее значение в некоторой точке
ее значение в некоторой точке ![]() вычисляется по схеме пп. 2.2.1 – 2.2.4.
вычисляется по схеме пп. 2.2.1 – 2.2.4.
4. Этап 4 - формирование области планирования
При использовании на этапе 2 симплекс-планов, симплексы ![]() ,
, ![]() ,…,
,…,![]() могут сформировать область, которая сильно вытянута и произвольно ориентированна в пространстве
могут сформировать область, которая сильно вытянута и произвольно ориентированна в пространстве ![]() (см. Рис. 4). Аналогично, при использовании регрессионных планов первого порядка, параллелепипеды
(см. Рис. 4). Аналогично, при использовании регрессионных планов первого порядка, параллелепипеды ![]() ,
, ![]() ,…,
,…,![]() могут сформировать такую же область. Поскольку качество аппроксимации существенно зависит от выбора области планирования [4], возникает задача определения этой области так, чтобы она была в некотором смысле оптимальной.
могут сформировать такую же область. Поскольку качество аппроксимации существенно зависит от выбора области планирования [4], возникает задача определения этой области так, чтобы она была в некотором смысле оптимальной.
В данном случае в качестве критерия оптимальности области планирования естественно использовать ее объем ![]() . Поэтому будем искать область планирования в виде параллелепипеда
. Поэтому будем искать область планирования в виде параллелепипеда ![]() , включающего в себя все симплексы
, включающего в себя все симплексы ![]() ,
, ![]() ,…,
,…,![]() или параллелепипеды
или параллелепипеды ![]() ,
, ![]() ,…,
,…,![]() и имеющего минимальный объем. Поскольку в области планирования
и имеющего минимальный объем. Поскольку в области планирования ![]() предполагается лишь вычисление значений вспомогательной аппроксимирующей функции
предполагается лишь вычисление значений вспомогательной аппроксимирующей функции ![]() , а не решение задачи (1), то при построении этой области можно опустить требование принадлежности параллелепипеда
, а не решение задачи (1), то при построении этой области можно опустить требование принадлежности параллелепипеда ![]() множеству
множеству ![]() .
.
Заметим, что в общей постановке задача построения области планирования является задачей построения выпуклой оболочки ![]() , где
, где ![]() ,
, ![]() - вершины симплексов
- вершины симплексов ![]() ,
, ![]() ,…,
,…,![]() или параллелепипедов
или параллелепипедов ![]() ,
, ![]() ,…,
,…,![]() [7,8].
[7,8].
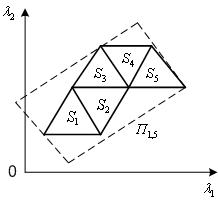
Рис. 4. К построению области планирования: ![]() ;
; ![]()
![]() ;
; ![]() - прямоугольная область планирования
- прямоугольная область планирования
Наряду с системой координат ![]() рассмотрим систему координат
рассмотрим систему координат ![]() , оси которой параллельны ребрам искомого параллелепипеда
, оси которой параллельны ребрам искомого параллелепипеда ![]() . Матрицу перехода от первой системы координат ко второй системе обозначим
. Матрицу перехода от первой системы координат ко второй системе обозначим ![]() , где
, где ![]() - косинус угла между ортами
- косинус угла между ортами ![]() ,
, ![]() указанных систем координат (здесь учтено, что множество допустимых значений
указанных систем координат (здесь учтено, что множество допустимых значений ![]() лежит в первом координатном угле системы координат
лежит в первом координатном угле системы координат ![]() ).
).
В результате задача отыскания оптимального параллелепипеда ![]() формализуется в виде многомерной задачи условной оптимизации
формализуется в виде многомерной задачи условной оптимизации
![]()
![]() =
=![]() , (8)
, (8)
где ![]() - объем искомого параллелепипеда
- объем искомого параллелепипеда ![]() , множество
, множество ![]() допустимых значений компонентов матрицы
допустимых значений компонентов матрицы ![]() определяется выражением
определяется выражением ![]() .
.
При фиксированной матрице ![]() вычисление объема параллелепипеда
вычисление объема параллелепипеда ![]() производится по следующей схеме:
производится по следующей схеме:
1) По формуле ![]() ,
, ![]() находим координаты всех векторов
находим координаты всех векторов ![]() в системе координат
в системе координат ![]() .
.
2) Поочередно для каждого из измерений находим минимальные и максимальные значения компонентов векторов ![]() ,
, ![]() :
:
![]() ,
, ![]() ,
, ![]() .
.
3) Вычисляем объем
![]() .
.
Поскольку критерий оптимальности ![]() является, вообще говоря, многоэкстремальным и частные производные его по компонентам матрицы A не известны, для решения задачи (8) следует использовать методы глобальной условной оптимизации [9].
является, вообще говоря, многоэкстремальным и частные производные его по компонентам матрицы A не известны, для решения задачи (8) следует использовать методы глобальной условной оптимизации [9].
Назовем метод формирования области планирования, схема которого рассмотрена выше, метод М4.1.
Замечание. Построенная методом М4.1 область планирования содержит, вообще говоря, как точки, принадлежащие симплексам ![]() ,
, ![]() ,…,
,…,![]() или параллелепипедам
или параллелепипедам ![]() ,
, ![]() ,…,
,…,![]() , так и точки не принадлежащие им. Погрешность аппроксимации функции
, так и точки не принадлежащие им. Погрешность аппроксимации функции ![]() в последних точках может значительно превышать погрешность аппроксимации во внутренних точках указанных симплексов и параллелепипедов (в этом случае правильнее было бы говорить не об аппроксимации, а об экстраполяции). Поэтому может оказаться целесообразным уменьшить объем параллелепипеда
в последних точках может значительно превышать погрешность аппроксимации во внутренних точках указанных симплексов и параллелепипедов (в этом случае правильнее было бы говорить не об аппроксимации, а об экстраполяции). Поэтому может оказаться целесообразным уменьшить объем параллелепипеда ![]() , что можно сделать по следующей схеме:
, что можно сделать по следующей схеме:
а) СМКО вычисляет суммарный объем ![]() симплексов
симплексов ![]() ,
, ![]() ,…,
,…,![]() или параллелепипедов
или параллелепипедов ![]() ,
, ![]() ,…,
,…,![]() ;
;
б) если отношение объемов ![]() , где
, где ![]() - свободный параметр метода, то СМКО уменьшает длины ребер параллелепипеда
- свободный параметр метода, то СМКО уменьшает длины ребер параллелепипеда ![]() - сжимает этот параллелепипед к его центру.
- сжимает этот параллелепипед к его центру.
Коэффициент сжатия может быть выбран на основе различных подходов, например, пропорционально текущей длине ребра, так, чтобы отношение указанных объемов было равно ![]() , и пр.
, и пр.
5. Этап 5 - аппроксимация вспомогательной функции
В данном разделе рассматривается задача аппроксимации вспомогательной функции ![]() , построенной любым из рассмотренных в п. 3 методов. В подразделе 5.1 рассматривается линейная аппроксимация этой функции на основе полного факторного эксперимента первого порядка, в подразделе 5.2 – линейная аппроксимация на основе регрессионных планов первого порядка [1], в подразделе 5.3 – аппроксимация квадратичной функцией на основе полного факторного эксперимента второго порядка, в подразделе 5.4 – квадратичная аппроксимация на основе ортогональных центрально-композиционных планов второго порядка [2], в подразделе 5.5 – аппроксимация квадратичной функцией на основе комбинации центрально-композиционных планов и композиционных планов Хартли и Вестлейка второго порядка [2].
, построенной любым из рассмотренных в п. 3 методов. В подразделе 5.1 рассматривается линейная аппроксимация этой функции на основе полного факторного эксперимента первого порядка, в подразделе 5.2 – линейная аппроксимация на основе регрессионных планов первого порядка [1], в подразделе 5.3 – аппроксимация квадратичной функцией на основе полного факторного эксперимента второго порядка, в подразделе 5.4 – квадратичная аппроксимация на основе ортогональных центрально-композиционных планов второго порядка [2], в подразделе 5.5 – аппроксимация квадратичной функцией на основе комбинации центрально-композиционных планов и композиционных планов Хартли и Вестлейка второго порядка [2].
Во всех случаях в качестве области планирования эксперимента используется параллелепипед ![]() . Для простоты записи сохраним за системой координат, в которой определен этот параллелепипед, прежние обозначения. Координаты его вершины обозначим векторами
. Для простоты записи сохраним за системой координат, в которой определен этот параллелепипед, прежние обозначения. Координаты его вершины обозначим векторами ![]() ,
, ![]() , где
, где ![]() - общее количество вершин. Координаты
- общее количество вершин. Координаты ![]() центра параллелепипеда
центра параллелепипеда ![]() определяются при этом формулой
определяются при этом формулой ![]() ,
, ![]() , где
, где ![]() ,
, ![]() . В результате нормированные (стандартные) факторы
. В результате нормированные (стандартные) факторы ![]() могут быть вычислены с помощью линейного преобразования
могут быть вычислены с помощью линейного преобразования 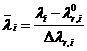 ,
, ![]() ,
, ![]() .
.
5.1. Аппроксимация линейной функцией на основе полного факторного эксперимента первого порядка (метод М5.1). Здесь, а также в следующем подразделе, результатом эксперимента является аппроксимирующая функция
![]()
![]() .
.
Схема эксперимента имеет следующий вид (см. подраздел 2.3).
1) СМКО строит план ПФЭ ![]() первого порядка с
первого порядка с ![]() точками и выполняет переход от стандартных факторов
точками и выполняет переход от стандартных факторов ![]() к «натуральным» факторам
к «натуральным» факторам ![]() ,
, ![]() .
.
2) Для каждой из полученных точек плана ![]() ,
,![]() СМКО вычисляет значение функции
СМКО вычисляет значение функции ![]() . Полученный
. Полученный ![]() -вектор обозначим
-вектор обозначим ![]() .
.
3) СМКО формирует, а затем решает СЛАУ ![]() , где
, где ![]() матрица
матрица ![]() - матрица Фишера, а
- матрица Фишера, а ![]() - искомый вектор оценок коэффициентов регрессии для стандартных факторов.
- искомый вектор оценок коэффициентов регрессии для стандартных факторов.
4) СМКО осуществляет проверку значимости оценок коэффициентов ![]() , а также вычисляет коэффициент детерминации
, а также вычисляет коэффициент детерминации ![]() [4].
[4].
Переход от вектора ![]() к вектору
к вектору ![]() осуществляется по формулам
осуществляется по формулам 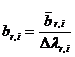 ,
, ![]() ,
, ![]() .
.
5.2. Аппроксимация линейной функцией на основе регрессионных планов первого порядка (метод М5.2). Эксперимента в данном случае выполняется по схеме предыдущего подраздела с тем отличием, что используемые планы эксперимента берутся
из библиотеки планов, рассмотренной в разделе 2 (это, преимущественно, планы ДФЭ ![]() ).
).
5.3. Аппроксимация квадратичной функцией на основе полного факторного эксперимента второго порядка. Для «натуральных» факторов ![]() и нормализованных факторов
и нормализованных факторов 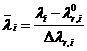 ,
, ![]() квадратичная регрессионная модель имеет, соответственно, вид [2]
квадратичная регрессионная модель имеет, соответственно, вид [2]
![]() , (9)
, (9)
![]() ,
,
где общее количество неизвестных коэффициентов равно ![]() . Переход от коэффициентов
. Переход от коэффициентов ![]() к коэффициентам
к коэффициентам ![]() осуществляется по формулам
осуществляется по формулам
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]()
![]() ,
, ![]() ,
,
где
![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() ;
;
![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() .
.
Схема эксперимента в этом случае аналогична схеме эксперимента, рассмотренной в подразделе 5.1, и имеет следующий вид (см. подраздел 2.3).
1) СМКО строит план ПФЭ ![]() второго порядка с
второго порядка с ![]() точками и выполняет переход от нормализованных факторов
точками и выполняет переход от нормализованных факторов ![]() к «натуральным» факторам
к «натуральным» факторам ![]() ,
, ![]() .
.
2) Для каждой из полученных точек плана ![]() ,
,![]() СМКО вычисляет значение функции
СМКО вычисляет значение функции ![]() - находит
- находит ![]() -вектор
-вектор ![]() .
.
3) СМКО формирует, а затем решает СЛАУ ![]() , где
, где ![]() матрица
матрица ![]() - матрица Фишера, а
- матрица Фишера, а ![]() - искомый вектор оценок коэффициентов регрессии для нормализованных факторов [2].
- искомый вектор оценок коэффициентов регрессии для нормализованных факторов [2].
4) СМКО осуществляет проверку значимости оценок коэффициентов регрессии ![]() , а также вычисляет коэффициент детерминации
, а также вычисляет коэффициент детерминации ![]() [4].
[4].
5.4. Аппроксимация квадратичной функцией на основе центрально-композиционных планов второго порядка (метод М5.4). На основе ортогональных центрально-композиционных планов (ЦКП) второго порядка разработана библиотека регрессионных планов для задачи многокритериальной оптимизации, содержащей от 2 до 10 частных критериев оптимальности [2]. Основные параметры библиотеки представлены в Табл. 2, где M – требуемое количество опытов, d - число базисных функций, ![]() - число степеней свободы.
- число степеней свободы.
Таблица 2. Основные параметры библиотечных планов на основе центрально-композиционных планов второго порядка
|
╧ п.п. |
m |
Ядро плана |
M |
d |
|
|
1 |
2 |
ПФЭ |
9 |
6 |
2 |
|
2 |
3 |
ПФЭ |
15 |
10 |
4 |
|
3 |
4 |
ПФЭ |
25 |
15 |
9 |
|
4 |
5 |
ДФЭ |
27 |
21 |
5 |
|
5 |
6 |
ДФЭ |
45 |
28 |
16 |
|
6 |
7 |
ДФЭ |
79 |
36 |
71 |
|
7 |
8 |
ДФЭ |
81 |
45 |
42 |
|
8 |
9 |
ДФЭ |
147 |
55 |
91 |
|
9 |
10 |
ДФЭ |
277 |
66 |
210 |
Напомним, что ЦКП являются не насыщенными планами и состоят из трех частей.
1. Основа плана или ядро плана – план ПФЭ ![]() или план ДФЭ
или план ДФЭ ![]() .
.
2. «Звездные» точки, расположенные на координатных осях на расстоянии ![]() от центра эксперимента, где величина
от центра эксперимента, где величина ![]() выбирается, исходя из того или иного критерия оптимальности регрессионного эксперимента.
выбирается, исходя из того или иного критерия оптимальности регрессионного эксперимента.
3. Центральная точка (мы рассматриваем только планы без дублирования опытов).
При использовании в качестве ядра плана ДФЭ ![]() , часть ЦКП, содержащая «звездные» точки и центральную точку, имеет вид, представленный в Табл. 3.
, часть ЦКП, содержащая «звездные» точки и центральную точку, имеет вид, представленный в Табл. 3.
Таблица 3. Часть ЦКП, содержащая «звездные» точки и центральную точку
|
Составные части ЦКП |
Номер опыта i |
|
|
… |
|
|
«Звездные точки» |
|
|
0 |
… |
0 |
|
|
|
0 |
… |
0 |
|
|
|
0 |
|
… |
0 |
|
|
|
0 |
|
… |
0 |
|
|
… |
… |
… |
… |
… |
|
|
|
0 |
0 |
… |
|
|
|
|
0 |
0 |
… |
|
|
|
Центральная точка |
|
0 |
0 |
… |
0 |
Для обеспечения ортогональности плана, величина ![]() выбирается равной
выбирается равной
![]() . (10)
. (10)
Схема эксперимента в этом случае аналогична схеме эксперимента, рассмотренной в подразделе 5.3.
5.5. Аппроксимация квадратичной функцией на основе центрально-композиционных планов и композиционных планов Хартли и Вестлейка второго порядка (метод М5.5). На основе слабо не насыщенных ЦКП и композиционных планов Хартли и Вестлейка второго порядка разработана библиотека регрессионных планов для задачи многокритериальной оптимизации, содержащей от 2 до 10 частных критериев оптимальности [2]. Основные параметры библиотеки представлены в Табл. 4, где M – требуемое количество опытов, d - число базисных функций, ![]() - число степеней свободы, КПХ- композиционный план Хартли, КПВ – композиционный план Вестлейка, НДР - нерегулярные дробные реплики. При
- число степеней свободы, КПХ- композиционный план Хартли, КПВ – композиционный план Вестлейка, НДР - нерегулярные дробные реплики. При ![]() в библиотеке использованы рассмотренные в предыдущем разделе ЦКП, при
в библиотеке использованы рассмотренные в предыдущем разделе ЦКП, при ![]() - планы Хартли или планы Вестлейка. В последних планах величина
- планы Хартли или планы Вестлейка. В последних планах величина ![]() определяется по формуле (10), что обеспечивает близость информационной матрицы Фишера к диагональной матрице.
определяется по формуле (10), что обеспечивает близость информационной матрицы Фишера к диагональной матрице.
Таблица 4. Основные параметры библиотечных планов на основе центрально-композиционных планов и композиционных планов Хартли и Вестлейка второго порядка
|
╧ п.п. |
m |
Наименование плана |
Ядро плана |
M |
d |
|
|
1 |
2 |
ЦКП |
ПФЭ |
7 |
6 |
2 |
|
2 |
3 |
ЦКП |
ПФЭ |
15 |
10 |
4 |
|
3 |
4 |
КПХ |
ПФЭ |
17 |
15 |
1 |
|
4 |
5 |
КПВ |
НДР 3* |
23 |
21 |
1 |
|
5 |
6 |
КПХ |
ДФЭ |
29 |
28 |
1 |
|
6 |
7 |
КПВ |
НДР 13* |
41 |
36 |
4 |
|
7 |
8 |
КПХ |
ДФЭ |
49 |
45 |
3 |
|
8 |
9 |
КПВ |
НДР 20* |
59 |
55 |
3 |
|
9 |
10 |
КПВ |
НДР 22* |
71 |
66 |
5 |
Схема эксперимента аналогична схеме эксперимента, рассмотренной в подразделе 5.3.
6. Этап 6 - определение начальной точки для следующей итерации
В подразделе 6.1 рассматривается определение начальной точки для следующей итерации в случае, когда аппроксимирующая функция ![]() является линейной (см. подразделы 5.1, 5.2), в подразделе 6.2 – в случае, когда эта функция является квадратичной (см. подразделы 5.3 - 5.5) [1, 2].
является линейной (см. подразделы 5.1, 5.2), в подразделе 6.2 – в случае, когда эта функция является квадратичной (см. подразделы 5.3 - 5.5) [1, 2].
6.1. Линейная аппроксимирующая функция ![]() (метод М6.1). Легко видеть, что если аппроксимирующая функция
(метод М6.1). Легко видеть, что если аппроксимирующая функция ![]() линейна, то ее градиент есть вектор
линейна, то ее градиент есть вектор ![]() =
=![]() . Таким образом, схема определения новой начальной точки
. Таким образом, схема определения новой начальной точки ![]() имеет следующий вид (см. подраздел 2.3).
имеет следующий вид (см. подраздел 2.3).
1) СМКО определяет компоненты вектора градиента функции ![]() в точке
в точке ![]()
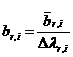 ,
, ![]() .
.
2) СМКО вычисляет текущую величину шага в направлении градиента ![]() , где
, где ![]() - свободный параметр метода, а величина
- свободный параметр метода, а величина ![]() выбирается из условия
выбирается из условия ![]() =
=![]() .
.
3) СМКО вычисляет координаты нового центра серии опытов
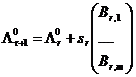 , где
, где 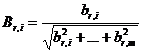 ,
, ![]() -
-
нормированные компоненты вектора градиента.
4) СМКО проверяет принадлежность точки ![]() множеству допустимых значений
множеству допустимых значений ![]() . Если
. Если ![]() , то СМКО полагает
, то СМКО полагает ![]() и переходит к следующей итерации. Если
и переходит к следующей итерации. Если![]() , то СМКО уменьшает длину текущего шага
, то СМКО уменьшает длину текущего шага ![]() , т.е. полагает
, т.е. полагает ![]() , где
, где ![]() - свободный параметр алгоритма, и переходит к п. 2.
- свободный параметр алгоритма, и переходит к п. 2.
6.2. Квадратичная аппроксимирующая функция ![]() (метод М6.2). Схема определения новой начальной точки имеет в данном случае следующий вид (см. подраздел 2.4).
(метод М6.2). Схема определения новой начальной точки имеет в данном случае следующий вид (см. подраздел 2.4).
1) СМКО определяет координаты ![]() точки максимума аппроксимирующей квадратичной функции
точки максимума аппроксимирующей квадратичной функции ![]() . Из выражения (9) для квадратичной регрессии следует, что координаты этой точки являются решением следующий СЛАУ
. Из выражения (9) для квадратичной регрессии следует, что координаты этой точки являются решением следующий СЛАУ
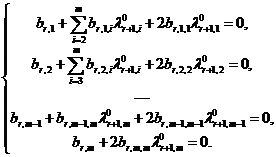
2) СМКО проверяет принадлежность точки ![]() множеству допустимых значений
множеству допустимых значений ![]() . Если
. Если ![]() , то СМКО полагает
, то СМКО полагает ![]() и переходит к следующей итерации. В противном случае, полагается
и переходит к следующей итерации. В противном случае, полагается ![]() и выполняется переход на начало данного пункта. Здесь
и выполняется переход на начало данного пункта. Здесь ![]() - свободный параметр метода.
- свободный параметр метода.
7. Заключение
На основе рассмотренных методов может быть построен широкий класс адаптивных алгоритмов решения задачи многокритериальной оптимизации.
В последующих работах данной серии предполагается, во-первых, на нескольких тестовых функциях исследовать погрешность аппроксимации и экстраполяции предлагаемых двухуровневых методов аппроксимации. Во-вторых, предполагается исследовать эффективность рассмотренных адаптивных человекомашинных методов решения задачи многокритериальной оптимизации на нескольких реальных прикладных задачах.
Задачу многомерной глобальной условной оптимизации (1) предполагается решать с помощью распределенных параллельных вычислительных систем. Как хорошо известно, одной из центральных проблем при этом является проблема согласования используемых алгоритмов с архитектурой вычислительной системы [10]. На основе рассмотренных в работе адаптивных человекомашинных методов решения задачи многокритериальной оптимизации может быть построено широкое множество алгоритмов решения этой задачи. Базируясь на этом множестве алгоритмов, предполагается, в-третьих, в программной системе «Парето» [11] реализовать идею параметрического согласования вычислительных алгоритмов с архитектурой используемой многопроцессорной вычислительной системы [12].
Литература
1. Карпенко А.П., Федорук В.Г. Адаптивные методы решения задачи многокритериальной оптимизации. 1. Методы на основе планов первого порядка. //“Наука и образование: электронное научное издание. Инженерное образование", www.technomag.edu.ru (╧ Гос. регистрации 0420700025, ЭЛ ╧ ФС 77-305 69), март, 2008, ╧0420800025/0007.
2. Карпенко А.П., Федорук В.Г. Адаптивные методы решения задачи многокритериальной оптимизации. 2. Методы на основе планов второго порядка. //"Наука и образование: электронное научное издание. Инженерное образование", www.technomag.edu.ru (╧ Гос. регистрации 0420700025, ЭЛ ╧ ФС 77-305 69), март, 2008, ╧0420800025/0008.
3. Карпенко А.П., Федорук В.Г. Адаптивные методы решения задачи многокритериальной оптимизации. 3. Методы на основе нейронных сетей и нечеткой логики. //"Наука и образование: электронное научное издание. Инженерное образование", www.technomag.edu.ru (╧ Гос. регистрации 0420700025, ЭЛ ╧ ФС 77-305 69), апрель, 2008.
4. Грачев Ю.П., Плаксин Ю.М. Математические методы планирования эксперимента. –М.: Изд-во «ДеЛи принт», 2005. - 296 с.
5. Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации. –М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. -440 с.
6. Потёмкин И.С. "Функциональные узлы цифровой автоматики", М.: Энергоатомиздат, 1988. – 320 с.
7. Ананий В. Левитин. Метод грубой силы: Поиск выпуклой оболочки //Алгоритмы: введение в разработку и анализ. -М.: Изд-во «Вильямс», 2006. - С. 157-157.
8. Половинкин Е. С, Балашов М. В. Элементы выпуклого и сильно выпуклого анализа. -М.: Физматлит, 2004. -416 с.
9. Жиелявский А.А., Жилинскас А.Г. Методы поиска глобального экстремума. - М.: Наука, 1991. – 247 с.
10. Воеводин В.В. Отображение проблем вычислительной математики на архитектуру вычислительных систем // Вычислительные методы и программирование, 2000, Т.1, с. 37-44.
11. Карпенко А.П., Федорук В.Г. Организация последовательно-параллельной обучающей системы многокритериальной оптимизации «Парето» //Материалы Всероссийской научной конференции, посвященной 75-летию Казанского Государственного технического Университета им. А.Н.Туполева «Информацион-ные технологии в науке, образовании и производстве», Казань, 2007, с. 618 – 620.
12. Карпенко А.П. Параметрическое согласование вычислительных алгоритмов с архитектурой многопроцессорных систем // Информационные технологии, 1996, ╧2, с. 36-39.
Публикации с ключевыми словами: адаптивные системы, многокритериальная оптимизация
Публикации со словами: адаптивные системы, многокритериальная оптимизация
Смотри также:
- Исследование погрешности аппроксимации многомерной функции с помощью нейронных сетей с радиальными базисными функциями
- Информационная модель и основные функции программной системы многокритериальной оптимизации ╚Парето╩
- Разработка модуля однокритериальной оптимизации для системы многокритериальной оптимизации ╚Парето╩
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



