научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#4 2008
УДК 519.6
Мухлисуллина Д.Т. (студентка 5 курса МГТУ им. Н.Э.Баумана,
E-mail: D.Mukhlisullina@mail.ru)
Введение
В
большинстве современных технических задач требуется обеспечить оптимальность
объекта проектирования одновременно по нескольким критериям оптимальности ![]() .
Обычно эти критерии противоречивы и оптимизация по каждому из них приводит к
различным значениям вектора варьируемых параметров Х. Поэтому выделяется
отдельный класс задач многокритериальной оптимизации.
.
Обычно эти критерии противоречивы и оптимизация по каждому из них приводит к
различным значениям вектора варьируемых параметров Х. Поэтому выделяется
отдельный класс задач многокритериальной оптимизации.
Будем
называть скалярные критерии оптимальности ![]() частными
критериями оптимальности, а совокупность частных критериев оптимальности Ф
частными
критериями оптимальности, а совокупность частных критериев оптимальности Ф![]() -
векторным критерием оптимальности. Обычно используют нормализованные
частные критерии. Будем полагать далее, что все частные критерии тем или иным
способом нормализованы.
-
векторным критерием оптимальности. Обычно используют нормализованные
частные критерии. Будем полагать далее, что все частные критерии тем или иным
способом нормализованы.
Задачу многокритериальной оптимизации будем условно записывать в виде
![]() Ф(X)=Ф
Ф(X)=Ф![]() ,
; &nb
sp;
(1)
,
; &nb
sp;
(1)
где ![]() -
множество допустимых значений вектора варьируемых параметров X,
вектор
-
множество допустимых значений вектора варьируемых параметров X,
вектор ![]() -
решение
задачи.
-
решение
задачи.
Еще сравнительно недавно считалось, что проблема многих критериев является некоторым сравнительно небольшим разделом теории оптимизации, задачей которого является сведение нескольких критериев выбора решения к единственному критерию. Проблема такого сведения решалась методами теорией многокритериальной полезности (Multi-Attribute Utility Theory, MAUT) [1,2]. В рамках MAUT предлагается выразить предпочтения Лица, Принимающего Решение (ЛПР), в виде функции полезности (ценности), аргументами которой являются рассматриваемые критерии, а затем найти допустимое решение, максимизирующее значение этой функции. Поскольку использовать теоретические построения MAUT на практике довольно затруднительно, при решении практических задач обычно просто задавали веса критериев, которые должны были отражать их важность. Далее взвешенные критерии (или, в самом сложном случае, некоторые функции от критериев) складывались, и получалась некоторая новая функция, которая использовалась в качестве единственного критерия оптимальности.
Метод STEM [1,2] базировался на принципиально иной основе. В этом методе были реализована прямая итеративная человеко-машинная процедура поиска решения, соответствующего предпочтениям ЛПР (STEp Method).
Основной принцип построения итеративных процедур заключается в выделение на каждой итерации двух этапов: этапа вычислений, осуществляемых компьютером, и этапа, на котором ЛПР выражает свои предпочтения. На первом этапе обычно компьютер решает некоторую задачу оптимизации, которая формируется на основе информации о предпочтениях ЛПР, полученной на предыдущих итерациях. На втором этапе ЛПР уточняет информацию о предпочтениях на основе анализа результатов расчета.
Задача,
рассматриваемая в данной работе, решается в связи с проблемой
аппроксимации «функции предпочтений» ЛПР при решении задачи многокритериальной
оптимизации с помощью прямой итеративной человеко-машинной процедуры [3].
Предполагается, что функция предпочтений ЛПР ψ(x)
определенна на множестве ![]() и
выполняет его отображение во множество действительных числе R, то есть
и
выполняет его отображение во множество действительных числе R, то есть
Ψ: X ![]() R.
R.
При этом задача многокритериальной оптимизации
сводится к задаче выбора вектора ![]() такого,
что
такого,
что
![]() ψ(X) = ψ
ψ(X) = ψ![]() .
.
Обозначим
операцию свертки частных критериев в скалярный критерий ![]() , где
, где ![]() – вектор
весовых множителей,
– вектор
весовых множителей, ![]() -
множество допустимых значений этого вектора. Отметим, что здесь не
фиксируется способ свертки, в принципе он может быть любым [4]. Иногда функцию
-
множество допустимых значений этого вектора. Отметим, что здесь не
фиксируется способ свертки, в принципе он может быть любым [4]. Иногда функцию ![]() в литературе называют
суперкритерием.
в литературе называют
суперкритерием.
Таким
образом, при каждом фиксированном векторе ![]() метод скалярной
свертки сводит решение многокритериальной задачи к решению однокритериальной
задачи глобальной условной оптимизации
метод скалярной
свертки сводит решение многокритериальной задачи к решению однокритериальной
задачи глобальной условной оптимизации
![]()
![]() =
= ![]() (2)
(2)
Отметим,
что в силу ограниченности и замкнутости множества ![]() решение задачи
(2) существует [3].
решение задачи
(2) существует [3].
Если
при каждом ![]() решение
задачи (2) единственно (а при использовании численных методов это всегда имеет
место), то условие (2) ставит в соответствие каждому из допустимых векторов
решение
задачи (2) единственно (а при использовании численных методов это всегда имеет
место), то условие (2) ставит в соответствие каждому из допустимых векторов ![]() единственный
вектор
единственный
вектор ![]() и
соответствующие значения частных критериев оптимальности
и
соответствующие значения частных критериев оптимальности ![]() .
Это обстоятельство позволяет полагать, что отношение предпочтения ЛПР
определено не на множестве
.
Это обстоятельство позволяет полагать, что отношение предпочтения ЛПР
определено не на множестве ![]() ,
а на множестве
,
а на множестве![]() ,
то есть
,
то есть
Ψ:
Λ ![]() R.
R.
В
результате задача многокритериальной оптимизации сводится к задаче выбора вектора
![]() такого,
что
такого,
что
![]() .
; &nb
sp; &
nbsp;
(3)
.
; &nb
sp; &
nbsp;
(3)
Величина
![]() полагается
лингвистической переменной со значениями ”Очень-очень плохо”, ”Очень
плохо”, …, ”Отлично”. Центры соответствующих нечетких множеств
обозначаются
полагается
лингвистической переменной со значениями ”Очень-очень плохо”, ”Очень
плохо”, …, ”Отлично”. Центры соответствующих нечетких множеств
обозначаются ![]() и
имеют четкие значения 1, 2, …, 9, соответственно.
и
имеют четкие значения 1, 2, …, 9, соответственно.
При аппроксимации функции предпочтений ЛПР с помощью нейронных сетей вместо
задачи (3) рассматривается задача отыскания вектора ![]() , обеспечивающего
максимальное значение четкой дискретной функции
, обеспечивающего
максимальное значение четкой дискретной функции ![]() :
:
![]() .
&nbs
p; &n
bsp;
(4)
.
&nbs
p; &n
bsp;
(4)
1. Нейронные сети с радиальными базисными функциями и их аппроксимирующие свойства
Искусственный
нейрон (далее - нейрон) обычно определяется как элемент, имеющий некоторое
количество входов (синапсов), на которые поступают входные сигналы ![]() и один
выход (аксон), с которого снимается выходной сигнал
и один
выход (аксон), с которого снимается выходной сигнал ![]() (см. Рис. 1).
(см. Рис. 1).
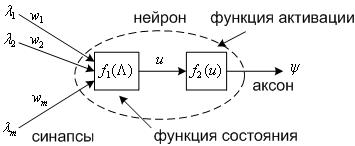
Рис. 1. К определению искусственного нейрона.
Функция состояния нейрона ![]() определяет
состояние нейрона в зависимости от его входов, весов входов
определяет
состояние нейрона в зависимости от его входов, весов входов ![]() и,
возможно, предыдущих состояний нейрона. Чаще всего используют следующие функции
состояния, не зависящие от предыдущего состояния [3].
и,
возможно, предыдущих состояний нейрона. Чаще всего используют следующие функции
состояния, не зависящие от предыдущего состояния [3].
1.
Скалярное
произведение векторов ![]()
![]() ,
; &nb
sp; &
nbsp;
(5)
,
; &nb
sp; &
nbsp;
(5)
2.
Расстояние
между векторами ![]() в
некоторой метрике, например,
в
некоторой метрике, например,
![]() ,
; &nb
sp; &
nbsp;
(6)
,
; &nb
sp; &
nbsp;
(6)
где ![]() -
положение центра функции
-
положение центра функции ![]() ,
,
![]() -
некоторая (обычно - евклидова) векторная норма.
-
некоторая (обычно - евклидова) векторная норма.
Искусственный нейрон с функцией состояния (5) называется персептроном, с функцией состояния (6) – нейроном с радиальной базисной функцией (RBF).
Часто функция состояния и функция активации объединяются в одну (передаточную) функцию. Далее мы будем следовать этому соглашению.
Нейронные сети (НС) образуются путем соединения синапсов одних нейронов с аксонами других. Важно, что возможно соединение многих синапсов нейронов с одним аксоном. Как правило, вид передаточных функций всех нейронов в сети фиксирован (используются однородные сети), а веса и, возможно, параметры передаточных функций могут изменяться.
Существуют НС с множеством различных топологий. Приведем классификацию основных многослойных сетей:
· сети без обратных связей (сети прямого распространения): многослойные персептроны; многослойные сети с радиальными базисными функциями;
· сети с обратными связями (рекуррентные сети): соревновательные сети; сети Кохонена; сети Хопфилда; сети Элмана; сети Жордана.
Минимальной реализацией нейронной сети является двухслойная НС, состоящая из входного (распределительного), промежуточного (скрытого) и выходного слоя (при подсчете числа слоев входной слой обычно не учитывается) - см. Рис. 2.
Обозначим выходы нейронов скрытого слоя ![]() . Тогда формально функционирование
нейронной сети, представленной на Рис. 2, описывается как суперпозиция функций
. Тогда формально функционирование
нейронной сети, представленной на Рис. 2, описывается как суперпозиция функций
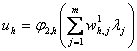 ,
, ![]() ,
,
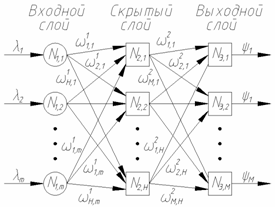
Рис.
2. Двухслойная
сеть без обратных связей: ![]() -
количество
нейронов во входном слое;
-
количество
нейронов во входном слое; ![]() -
количество
нейронов в скрытом слое;
-
количество
нейронов в скрытом слое; ![]() -
количество
нейронов в выходном слое.
-
количество
нейронов в выходном слое.
![]() ,
, ![]() .
.
Здесь ![]() -
передаточная функция нейрона
-
передаточная функция нейрона ![]() ,
,
![]() -
передаточная функция нейрона
-
передаточная функция нейрона ![]() .
.
Нейронная сеть на основе RBF-нейронов является частным случаем двухслойной сети прямого распространения и моделирует произвольную нелинейную функцию с помощью одного промежуточного слоя. Выходной слой сети строится на основе нейронов с линейными передаточными функциями. Последнее обстоятельство позволяет не обучать нейроны выходного слоя.
Рассмотрим случай, когда число элементов в обучающей выборке относительно
невелико (не превышает нескольких сотен). При этом в RBF-сети
каждому вектору ![]() можно
поставить в соответствие свой нейрон с центром в точке
можно
поставить в соответствие свой нейрон с центром в точке ![]() , т.е. принять
, т.е. принять ![]() . Таким образом,
в данном случае RBF-сеть содержит
один выходной нейрон и N
= H нейронов в скрытом
слое; веса
. Таким образом,
в данном случае RBF-сеть содержит
один выходной нейрон и N
= H нейронов в скрытом
слое; веса ![]() равны
единице. Функционирование такой сети описывается следующей формулой
равны
единице. Функционирование такой сети описывается следующей формулой
![]() ,
, 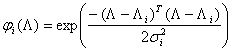 ,
;
(7)
,
;
(7)
где ![]() -
величина, характеризующая “ширину” колокола функции
-
величина, характеризующая “ширину” колокола функции ![]() .
.
В
данной работе предполагается, что величины ![]() фиксированы,
тогда задача нахождения весов в формуле (7) сводится к решению СЛАУ
фиксированы,
тогда задача нахождения весов в формуле (7) сводится к решению СЛАУ
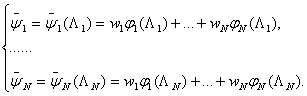 &nbs
p;
(8)
&nbs
p;
(8)
Здесь ![]() - выход
нейронной сети, соответствующий входному вектору
- выход
нейронной сети, соответствующий входному вектору ![]() ,
, ![]() . Заметим,
что из определения передаточной функции
. Заметим,
что из определения передаточной функции ![]() следует, что
следует, что ![]() .
.
Решение СЛАУ (8) сводится к обращению ![]() матрицы
матрицы
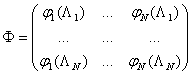 .
.
Если величины ![]() не
фиксированы, то помимо весов необходимо определить еще и эти величины. В этом
случае задача обучения сети становится нелинейной, и решать ее приходится с
использованием итеративных численных методов оптимизации, например, градиентных
методов.
не
фиксированы, то помимо весов необходимо определить еще и эти величины. В этом
случае задача обучения сети становится нелинейной, и решать ее приходится с
использованием итеративных численных методов оптимизации, например, градиентных
методов.
Аппроксимация функций нейронными сетями основана на следующей теореме.
Теорема. Пусть множество ![]() -
замкнуто и ограничено, функция
-
замкнуто и ограничено, функция ![]() принадлежит
классу непрерывных на множестве
принадлежит
классу непрерывных на множестве ![]() функций.
Тогда эта функция может быть равномерно приближена функциями вычислимыми с
помощью нейросети [6].
функций.
Тогда эта функция может быть равномерно приближена функциями вычислимыми с
помощью нейросети [6].
2. Тестовая функций и область планирования эксперимента
Пусть
![]() ,
, ![]() },
},
![]() .
; &nb
sp; &
nbsp;
(9)
.
; &nb
sp; &
nbsp;
(9)
Выберем
коэффициенты ![]() из
условий
из
условий ![]() ,
,
![]() . Тогда
. Тогда ![]() . В результате такого задания
функции
. В результате такого задания
функции ![]() она
приобретает на множестве
она
приобретает на множестве ![]() все
значения от 1 до 9. Максимум этой функции, равный 9, достигается в точке
все
значения от 1 до 9. Максимум этой функции, равный 9, достигается в точке ![]() .
.
Перейдем к стандартным факторам ![]() .
Для этого положим, что
.
Для этого положим, что 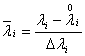 ,
,![]() , где
, где ![]() - основной
(базовый) уровень фактора
- основной
(базовый) уровень фактора ![]() ,
а
,
а ![]() - шаг
варьирования этого фактора. В качестве центральной точки плана примем точку
- шаг
варьирования этого фактора. В качестве центральной точки плана примем точку ![]() .
Все шаги
.
Все шаги ![]() варьирования
факторов положим одинаковыми и равными 0.125. Тогда имеем:
варьирования
факторов положим одинаковыми и равными 0.125. Тогда имеем:
![]() .
;
(10)
.
;
(10)
Область планирования эксперимента при этом есть гиперкуб ![]() ,
,
![]() .
.
В
качестве желаемой функции будем использовать функцию ![]() .
.
3. Организация эксперимента
Для
оценки точности аппроксимации будем использовать ![]() случайных
точек, равномерно распределенных в гиперкубе
случайных
точек, равномерно распределенных в гиперкубе ![]() . Будем эти точки
называть контрольными точками. Совокупность контрольных точек,
принадлежащих гиперкубу
. Будем эти точки
называть контрольными точками. Совокупность контрольных точек,
принадлежащих гиперкубу ![]() ,
обозначим
,
обозначим ![]() ,
,
![]() .
.
Для оценки точности экстраполяции будем использовать следующие области планирования эксперимента:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Количество контрольных точек в этих областях обозначим ![]() ,
, ![]() ,
, ![]() ,
соответственно;
,
соответственно; ![]() .
.
Так же, как при оценке точности аппроксимации, для проверки точности
экстраполяции будем использовать случайные точки, равномерно распределенные в
гиперкубе ![]() ,
,
![]() и
соответствующие множества контрольных точек
и
соответствующие множества контрольных точек ![]() ,
, ![]() ,
, ![]() .
.
Введем в рассмотрение также следующие множества контрольных точек:
·
множество
точек ![]() ,
, ![]() , которое
содержит контрольные точки разности
, которое
содержит контрольные точки разности ![]() множеств
этих точек
множеств
этих точек ![]() ,
, ![]() ;
;
·
аналогичное
множество точек ![]() ;
;
·
аналогичное
множество точек ![]() ;
;
·
аналогичное
множество точек ![]() .
.
Количества точек множества ![]() , принадлежащих
указанным множествам, обозначим
, принадлежащих
указанным множествам, обозначим ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Построение аппроксимирующей функции будем выполнять на основе центральных композиционных планов (ЦКП), которые являются не насыщенными планами и состоят из трех частей [7].
1)
Основа плана или ядро плана – полный факторный эксперимент ПФЭ ![]() или
дробный факторный эксперимент ДФЭ
или
дробный факторный эксперимент ДФЭ ![]() .
.
2)
«Звездные» точки (2m
штук),
расположенные на координатных осях на расстоянии ![]() от центра
эксперимента. Величину
от центра
эксперимента. Величину ![]() будем
выбирать, исходя из требования ортогональности плана. При этом
будем
выбирать, исходя из требования ортогональности плана. При этом
![]() ,
,
где
![]() -
общее количество опытов.
-
общее количество опытов.
3) Центральная точка.
Заметим, что ![]() ,
если в качестве ядра плана используется ПФЭ
,
если в качестве ядра плана используется ПФЭ ![]() . Если в качестве ядра
используется ДФЭ
. Если в качестве ядра
используется ДФЭ ![]() ,
то
,
то ![]() -
количество точек, исключенных из ПФЭ
-
количество точек, исключенных из ПФЭ ![]() .
.
Ниже перечисляются используемые планы:
1)
m=2 (см. Табл. 1). Ядро плана – план
ПФЭ ![]() . p=0.
Число опытов
. p=0.
Число опытов ![]() .
Число степеней свободы
.
Число степеней свободы ![]() .
.
Таблица
1.
План на основе плана ПФЭ ![]() .
.
|
Номер опыта i |
|
|
|
1 |
-1 |
-1 |
|
2 |
1 |
-1 |
|
4 |
-1 |
1 |
|
3 |
1 |
1 |
|
5 |
|
0 |
|
6 |
|
0 |
|
7 |
0 |
|
|
8 |
0 |
|
|
9 |
0 |
0 |
2)
m=3 (см. Табл.
2). Ядро плана – план ПФЭ ![]() . p=0. Число опытов
N=15. Число
степеней свободы
. p=0. Число опытов
N=15. Число
степеней свободы ![]() 4.
4.
Таблица 2. План на основе
плана ПФЭ ![]() .
.
|
I |
|
|
|
|
1 |
-1 |
-1 |
-1 |
|
2 |
1 |
-1 |
-1 |
|
3 |
-1 |
1 |
-1 |
|
4 |
1 |
1 |
-1 |
|
5 |
-1 |
-1 |
1 |
|
6 |
1 |
-1 |
1 |
|
7 |
-1 |
1 |
1 |
|
8 |
1 |
1 |
1 |
|
9 |
|
0 |
0 |
|
10 |
|
0 |
0 |
|
11 |
0 |
|
0 |
|
12 |
0 |
|
0 |
|
13 |
0 |
0 |
|
|
14 |
0 |
0 |
|
|
15 |
0 |
0 |
0 |
3)
m=4 (см. Табл.
3). Ядро плана – план ПФЭ ![]() . p=0. Число опытов
N=25. Число
степеней свободы
. p=0. Число опытов
N=25. Число
степеней свободы ![]() 9.
9.
4)
m=5. Ядро плана –
план ДФЭ ![]() . p=1. Число опытов
N=27. Число
степеней свободы
. p=1. Число опытов
N=27. Число
степеней свободы ![]() 5. Ведущие
факторы:
5. Ведущие
факторы: ![]() . Генерирующее соотношение:
. Генерирующее соотношение: ![]() .
.
5)
m=6. Ядро плана –
план ДФЭ ![]() . p=1. Число опытов
N=45. Число
степеней свободы
. p=1. Число опытов
N=45. Число
степеней свободы ![]() 16. Ведущие
факторы:
16. Ведущие
факторы: ![]() . Генерирующее соотношение:
. Генерирующее соотношение: ![]() .
.
6)
m=7. Ядро плана –
план ДФЭ ![]() . p=1. Число опытов
N=79. Число
степеней свободы
. p=1. Число опытов
N=79. Число
степеней свободы ![]() 71. Ведущие
факторы:
71. Ведущие
факторы: ![]() . Генерирующее соотношение:
. Генерирующее соотношение: ![]() .
.
Таблица
3.
План на основе плана ПФЭ ![]() .
.
|
I |
|
|
|
|
|
1 |
-1 |
-1 |
-1 |
-1 |
|
2 |
1 |
-1 |
-1 |
-1 |
|
3 |
-1 |
1 |
-1 |
-1 |
|
4 |
1 |
1 |
-1 |
-1 |
|
5 |
-1 |
-1 |
1 |
-1 |
|
6 |
1 |
-1 |
1 |
-1 |
|
7 |
-1 |
1 |
1 |
-1 |
|
8 |
1 |
1 |
1 |
-1 |
|
9 |
-1 |
-1 |
-1 |
1 |
|
10 |
1 |
-1 |
-1 |
1 |
|
11 |
-1 |
1 |
-1 |
1 |
|
12 |
1 |
1 |
-1 |
1 |
|
13 |
-1 |
-1 |
1 |
1 |
|
14 |
1 |
-1 |
1 |
1 |
|
15 |
-1 |
1 |
1 |
1 |
|
16 |
1 |
1 |
1 |
1 |
|
17 |
|
0 |
0 |
0 |
|
18 |
|
0 |
0 |
0 |
|
19 |
0 |
|
0 |
0 |
|
20 |
0 |
|
0 |
0 |
|
21 |
0 |
0 |
|
0 |
|
22 |
0 |
0 |
|
0 |
|
23 |
0 |
0 |
0 |
|
|
24 |
0 |
0 |
0 |
|
|
25 |
0 |
0 |
0 |
0 |
7)
m=8. Ядро плана –
план ДФЭ ![]() . p=2. Число опытов
N=81. Число
степеней свободы
. p=2. Число опытов
N=81. Число
степеней свободы ![]() 42. Ведущие
факторы:
42. Ведущие
факторы: ![]() . Генерирующие соотношения:
. Генерирующие соотношения: ![]() ,
, ![]() .
.
8)
m=9. Ядро плана –
план ДФЭ ![]() . p=2. Число опытов
N=147. Число
степеней свободы
. p=2. Число опытов
N=147. Число
степеней свободы ![]() 91. Ведущие
факторы:
91. Ведущие
факторы: ![]() . Генерирующие соотношения:
. Генерирующие соотношения: ![]() ,
, ![]() .
.
9)
m=10. Ядро плана
– план ДФЭ ![]() . p=2. Число опытов
N=277. Число
степеней свободы
. p=2. Число опытов
N=277. Число
степеней свободы ![]() 210. Ведущие
факторы:
210. Ведущие
факторы: ![]() . Генерирующие соотношения:
. Генерирующие соотношения: ![]() ,
, ![]() .
.
4. Исследование погрешности аппроксимации
Исследование выполнены с помощью программы MathCAD. На приведенных ниже графиках графики синего цвета – регрессии 2-го порядка, полученные с помощью функции regress() системы MathCAD.
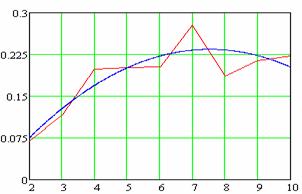
Рис.
3.
Максимальная относительная погрешность аппроксимации, как функция размерности
задачи ![]()
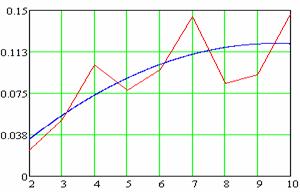
Рис.
4.
Математическое ожидание относительной погрешности аппроксимации, как функция
размерности задачи ![]()
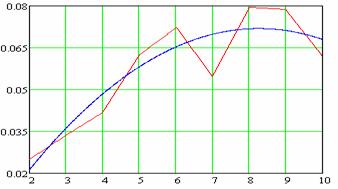
Рис.
5.
Среднее квадратичное отклонение относительной погрешности аппроксимации, как
функция размерности задачи ![]()

Рис.
6.
Относительная погрешность аппроксимации, как функция номера опыта (множество ![]() )
)
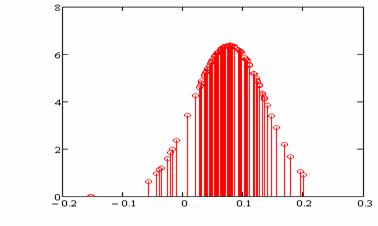
Рис.
7.
Плотность распределения относительной погрешности аппроксимации для множества ![]() .
.
5. Исследование точности экстраполяции
Исследование
точности экстраполяции выполняется по той же схеме, что и исследование точности
аппроксимации. Отличие состоит в том, что вычисляется только оценка
максимальной погрешности экстраполяции и эти вычисления производятся на
множествах ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Во
всех случаях множество точек ![]() ,
,
![]() содержит
количество случайных точек, пропорциональное объему этого множества. Поэтому
количество случайных точек по каждому из измерений полагается равным
содержит
количество случайных точек, пропорциональное объему этого множества. Поэтому
количество случайных точек по каждому из измерений полагается равным ![]() . Таким образом,
множество
. Таким образом,
множество ![]() будет
содержать всего 200 точек, множество
будет
содержать всего 200 точек, множество ![]() -
300 точек, …, множество
-
300 точек, …, множество ![]() -
1000 точек. Заметим, что это соглашение означает, что при генерации, например,
множества
-
1000 точек. Заметим, что это соглашение означает, что при генерации, например,
множества ![]() придется
придется
![]() раз
генерировать случайные числа, равномерно распределенные в интервале [-1.4,1.4].
раз
генерировать случайные числа, равномерно распределенные в интервале [-1.4,1.4].
Приняты
следующие обозначения: EpsMax(B/A)
– максимальная относительная погрешность экстраполяции на множестве ![]() , EpsMax(C/B)
– на множестве
, EpsMax(C/B)
– на множестве ![]() ,
EpsMax(D/C)
– на множестве
,
EpsMax(D/C)
– на множестве ![]() .
.
Таблица 4. Результаты исследования точности экстраполяции
|
m |
EpsMax(B/A) |
EpsMax(C/B) |
EpsMax(D/C) |
|
2 |
0.095 |
0.135 |
0.148 |
|
3 |
0.17 |
0.119 |
0.295 |
|
4 |
0.179 |
0.222 |
0.257 |
|
5 |
0.637 |
0.638 |
0.763 |
|
6 |
0.619 |
0.574 |
0.699 |
|
7 |
0.643 |
0.634 |
0.643 |
|
8 |
0.817 |
0.775 |
0.817 |
|
9 |
0.722 |
0.715 |
0.722 |
|
10 |
0.738 |
0.738 . |
0.738 |
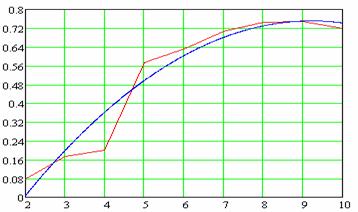
Рис.
8.
Максимальная погрешность экстраполяции на множестве ![]() как функция
размерности задачи
как функция
размерности задачи ![]()
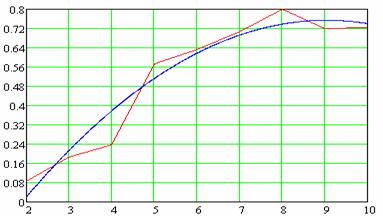
Рис.
9.
Максимальной погрешности экстраполяции на множестве ![]() как функция
размерности задачи
как функция
размерности задачи ![]()
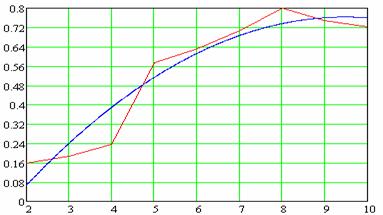
Рис.
10.
Максимальной погрешности экстраполяции на множестве ![]() как функция
размерности задачи
как функция
размерности задачи ![]() .
.
6. Исследование чувствительности к изменению количества точек в плане
Для ![]() выполняется серия из
выполняется серия из ![]() экспериментов по следующей схеме:
экспериментов по следующей схеме:
·
(![]() ) построение аппроксимирующей функции на
основе соответствующего плана, из которого удалены указанные ниже строки.
) построение аппроксимирующей функции на
основе соответствующего плана, из которого удалены указанные ниже строки.
|
|
|
|
…. |
|
|
1 |
- |
0 |
…. |
0 |
|
2 |
|
0 |
…. |
0 |
·
Оценка
относительной погрешности аппроксимации ![]() .
.
·
(![]() ) построение аппроксимирующей функции на
основе соответствующего плана, из которого удалены строки, указанные в
предыдущем пункте, плюс указанные ниже строки
) построение аппроксимирующей функции на
основе соответствующего плана, из которого удалены строки, указанные в
предыдущем пункте, плюс указанные ниже строки
|
|
|
|
…. |
|
|
1 |
0 |
- |
…. |
0 |
|
2 |
0 |
|
…. |
0 |
·
Оценка
относительной погрешности аппроксимации ![]() .
.
· …
·
(![]() ) построение аппроксимирующей функции на
основе соответствующего плана, из которого удалены строки, указанные в
предыдущих пунктах, плюс указанные ниже строки
) построение аппроксимирующей функции на
основе соответствующего плана, из которого удалены строки, указанные в
предыдущих пунктах, плюс указанные ниже строки
|
|
|
|
…. |
|
|
1 |
0 |
0 |
…. |
- |
|
2 |
0 |
0 |
…. |
|
·
Оценка
относительной погрешности аппроксимации ![]() .
.
Здесь K - количество точек, удаленных из соответствующего плана.
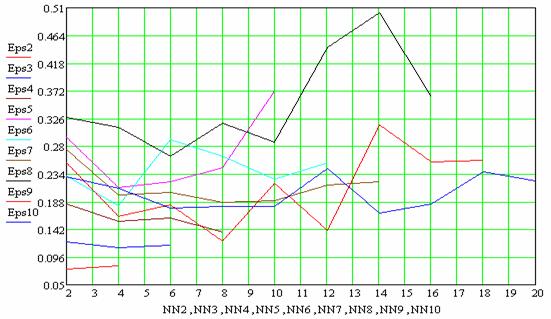
Рис. 11. Максимальная относительная погрешность аппроксимации
7. Заключение
Из проведенного исследования можно сделать вывод, что аппроксимирующие и экстраполирующие свойства нейронных сетей с радиальными базисными функциями существенно меняются с изменением количества точек в плане. На основе приведенных результатов можно утверждать, что эта зависимость является примерно квадратичной.
Литература
1. R.Benayuon, J.de Montgolfier, J.Terny, and O.I.Larichev. Linear Programming with Multiple Objective Functions: Step Method (STEM). Mathematical Programming, 1971, V. 1, No. 3, 366-375 с.
2. Р.Бенайюн, О.И.Ларичев, Ж.Монгольфье, Ж.Терни. Линейное программирование при многих критериях. Автоматика и телемеханика, 1971, ╧ 8.
3. Карпенко А.П., Федорук В.Г. Адаптивные методы решения задачи многокритериальной оптимизации. 1. Методы на основе планов первого порядка. //“Наука и образование: электронное научное издание. Инженерное образование", www.technomag.edu.ru (╧ Гос. регистрации 0420700025, ЭЛ ╧ ФС 77-305 69), март, 2008, ╧0420800025/0007.
4. Карпенко А.П., Федорук В.Г. Адаптивные методы решения задачи многокритериальной оптимизации. 2. Методы на основе планов второго порядка. //"Наука и образование: электронное научное издание. Инженерное образование", www.technomag.edu.ru (╧ Гос. регистрации 0420700025, ЭЛ ╧ ФС 77-305 69), март, 2008, ╧0420800025/0008.
5. Черноруцкий И.Г. Методы принятия решений. – СПб.: БХВ-Петербург. 2005. – 416 с.
6. Ларичев О.И. теория и методы принятия решения. -М.: Университетская книга, Логос, 2006. -392 с.
7. Загоруйко Н.Г. Прикладные методы анализа данных и знаний, Новосибирск, Изд-во Ин-та математики, 1999 г.-270 с.
8. Грачев Ю.П., Плаксин Ю.М. Математические методы планирования эксперимента. –М.: Издательство ДеЛипринт, 2005. - 296 с.
Публикации с ключевыми словами: многокритериальная оптимизация
Публикации со словами: многокритериальная оптимизация
Смотри также:
- Информационная модель и основные функции программной системы многокритериальной оптимизации ╚Парето╩
- Адаптивные методы решения задачи многокритериальной оптимизации, использующие аппроксимацию функции предпочтений лица, принимающего решения
- Разработка модуля однокритериальной оптимизации для системы многокритериальной оптимизации ╚Парето╩
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



