научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#2 февраль 2007
Мухлисуллина Д.Т. (студент 4 курса МГТУ им. Н.Э.Баумана,
E-mail: D.Mukhlisullina@mail.ru)
Введение
При решении современных задач оптимизации, как правило, приходится учитывать различные противоречивые требования, поэтому выделяют целый класс задач многоцелевой или многокритериальной оптимизации (МКО).
В задаче однокритериального принятия решений в условиях
определенности полагается, что на множестве ![]() задана критериальная
функция
задана критериальная
функция ![]() .
Выбор наилучшей альтернативы сводится к отысканию альтернативы с наименьшим
значением критериальной функции. Функция
.
Выбор наилучшей альтернативы сводится к отысканию альтернативы с наименьшим
значением критериальной функции. Функция ![]() в этом случае, называется критерием
(критерием качества, критерием оптимальности, целевой функцией, функцией
предпочтения, функцией полезности и т.п.). Критерий оптимальности может быть
как количественным (принимать числовые значения), так и качественным
(лингвистическим) - принимать значения типа «много», «мало» и пр. Типичными для
технических задач являются количественные критерии.
в этом случае, называется критерием
(критерием качества, критерием оптимальности, целевой функцией, функцией
предпочтения, функцией полезности и т.п.). Критерий оптимальности может быть
как количественным (принимать числовые значения), так и качественным
(лингвистическим) - принимать значения типа «много», «мало» и пр. Типичными для
технических задач являются количественные критерии.
В задаче многокритериального принятия решений предполагается,
что задана вектор-функция ![]() , и ЛПР желательно найти альтернативу,
которая, например, минимизировала бы все компоненты этой вектор-функции.
Компоненты
, и ЛПР желательно найти альтернативу,
которая, например, минимизировала бы все компоненты этой вектор-функции.
Компоненты ![]() вектор
- функции
вектор
- функции ![]() называются
частными критериями оптимальности.
называются
частными критериями оптимальности.
При решении задачи МКО ЛПР, принимая некоторую альтернативу ![]() в
качестве решения, всегда должно идти на компромисс - допуская ухудшение
значений одних частных критериев для улучшения значений других критериев.
Вследствие этого обстоятельства, деятельность ЛПР при решении МКО-задачи
является плохо формализуемой и требует привлечения его предыдущего опыта и
интуиции.
в
качестве решения, всегда должно идти на компромисс - допуская ухудшение
значений одних частных критериев для улучшения значений других критериев.
Вследствие этого обстоятельства, деятельность ЛПР при решении МКО-задачи
является плохо формализуемой и требует привлечения его предыдущего опыта и
интуиции.
Можно выделить следующие особенности современных задач оптимизации [1]:
· высокая размерность вектора альтернатив X (порядка 100);
·
сложная
структура множества допустимых альтернатив ![]() ,
обуславливаемая большим количеством (порядка 100) и нелинейностью
ограничивающих функций, формирующих это множество;
,
обуславливаемая большим количеством (порядка 100) и нелинейностью
ограничивающих функций, формирующих это множество;
·
высокая
размерность критериальной вектор - функции ![]() (порядка
100);
(порядка
100);
· высокая сложность математических моделей оптимизируемых технических систем (дифференциальные уравнения в частных производных и пр.);
· сложная топология частных критериев оптимальности (овражность, многоэкстремальность и пр.).
Решение таких задач не возможно без привлечения программных систем многокритериальной оптимизации (МКО-систем).
1. Постановка задачи многокритериальной оптимизации
В условиях определенности МКО-задачу запишем в следующем виде
&nb
sp; &
nbsp;
![]() ,
&nbs
p; &n
bsp;
(1)
,
&nbs
p; &n
bsp;
(1)
где ![]() - вектор переменных, принадлежащий
непустому замкнутому (компактному) множеству допустимых значений
- вектор переменных, принадлежащий
непустому замкнутому (компактному) множеству допустимых значений ![]() ;
; ![]() - вектор
частных критериев оптимальности, осуществляющий отображение множества
- вектор
частных критериев оптимальности, осуществляющий отображение множества ![]() в
непустое критериальное множество
в
непустое критериальное множество ![]() ;
; ![]() - искомое решение задачи;
- искомое решение задачи; ![]() -
арифметические векторные пространства размерности
-
арифметические векторные пространства размерности ![]() и
и ![]() , соответственно; T – символ транспонирования.
, соответственно; T – символ транспонирования.
Множество ![]() обычно задается с помощью
обычно задается с помощью ![]() ограничивающих
функций
ограничивающих
функций ![]()
![]() .
&nbs
p; &n
bsp; (2)
.
&nbs
p; &n
bsp; (2)
В условиях неопределенности критериальная вектор-функция ![]() и, может быть,
ограничивающие функции
и, может быть,
ограничивающие функции ![]() зависят кроме вектора переменных X
также от векторного фактора неопределенности
зависят кроме вектора переменных X
также от векторного фактора неопределенности ![]() , значения компонентов которого
неизвестны в момент принятия решения. Здесь
, значения компонентов которого
неизвестны в момент принятия решения. Здесь ![]() - множество допустимых
значений фактора неопределенности.
- множество допустимых
значений фактора неопределенности.
2. Структура системы многокритериальной оптимизации «Парето»
Система поддерживает следующие основные группы функций [1]:
·
приближенное
построение и визуализация множеств ![]() ,
, ![]() ;
;
· решения задачи многокритериальной оптимизации (1) априорными методами;
· решения задачи многокритериальной оптимизации (1) апостериорными методами;
· решения задачи многокритериальной оптимизации (1) адаптивными методами.
В зависимости от вычислительной сложности критерия
оптимальности ![]() , перечисленные функции могут выполняться в
последовательном или параллельном режимах. Параллельная реализация направлена
на использование вычислительного кластера с библиотекой MPI
в качестве коммуникационной среды.
, перечисленные функции могут выполняться в
последовательном или параллельном режимах. Параллельная реализация направлена
на использование вычислительного кластера с библиотекой MPI
в качестве коммуникационной среды.
Основные сущности системы «Парето»:
· пользователь;
· метазадача (в число атрибутов входит постановка общей задачи многокритериальной оптимизации);
· задача (в число атрибутов входит ее содержательное описание);
· модель (включая формальную постановку задачи);
· исследование (включая список соответствующих экспериментов);
· эксперимент (включая все параметры эксперимента его результаты);
· результаты эксперимента (включая параметры использованной вычислительной системы);
· многокритериальный метод (включая его содержательное описание);
· многокритериальный алгоритм (включая его формальное описание);
· многокритериальная программа (включая описание входов-выходов);
· аналогично, однокритериальный метод, однокритериальный алгоритм, однокритериальная программа;
· аналогично, вспомогательный метод, вспомогательный алгоритм, вспомогательный программа;
· глоссарий.
Система «Парето» содержит обучающую подсистему, которая может быть использована для самостоятельного изучения пользователем методов и алгоритмов многокритериальной оптимизации, а также для проведения лабораторных работ в этой области.
Основные модули системы «Парето»:
1) Группа модулей «Рабочее место» реализуют интерфейсную часть системы, представляют собой клиентское приложение и включает в себя следующие модули:
· модуль редактирования параметров основных сущностей системы, позволяющий путем последовательного заполнения полей сформировать соответствующую сущность системы;
· модуль защиты, обеспечивающий защиту от использования незарегистрированной копии программы;
· модуль регистрации/авторизации, позволяющий регистрироваться и авторизоваться уже зарегистрированным пользователям в системе;
· модуль работы с базой данных (БД), представляющий собой редактируемый список БД системы;
· модуль администрирования, доступный только пользователям, авторизованным с уровнем доступа «Администратор». Модуль позволяет редактировать все параметры системы, кроме тех, которые защищены мастер – паролем;
· модуль визуализации множества Парето;
· модуль «Help», позволяющий получить справку о системе.
2) Модуль анализа распределения вычислительных мощностей.
3) Вычислительный модуль.
3. Постановка задачи однокритериальной оптимизации
Однокритериальная задача условной оптимизации имеет вид
![]() , &n
bsp;
(3)
, &n
bsp;
(3)
где ![]() - множество допустимых значений
вектора параметров X, определяемое с
помощью вектора ограничивающих функций
- множество допустимых значений
вектора параметров X, определяемое с
помощью вектора ограничивающих функций ![]() :
:
![]() .
&nbs
p;
&nbs
p;
(4)
.
&nbs
p;
&nbs
p;
(4)
В формуле (3) ![]() - скалярный критерий оптимальности,
- скалярный критерий оптимальности, ![]() -
оптимальное значение вектора параметров,
-
оптимальное значение вектора параметров, ![]() - оптимальное значение критерия
оптимальности.
- оптимальное значение критерия
оптимальности.
Задачи оптимизации вида (3) решаются с помощью поискового метода оптимизации, если используется следующая процедура поиска вектора Х*:
· по очереди производятся испытания в точках
![]() ,
, ![]()
![]() ,
(5)
,
(5)
где ![]() -
начальное приближение,
-
начальное приближение, ![]() - некоторая
функция (заданная, возможно, не формулой, а алгоритмом);
- некоторая
функция (заданная, возможно, не формулой, а алгоритмом);
·
в
качестве решения задачи берется вектор ![]() , который
находится из условия
, который
находится из условия
![]()
![]()
4. Основные используемые методы и алгоритмы
4.1. Алгоритм генерации случайной сетки. Пусть ![]() -
последовательность случайных чисел, равномерно расположенных в интервале
-
последовательность случайных чисел, равномерно расположенных в интервале ![]() . Преобразуем
эту последовательность в координаты первого узла искомой сетки по формулам
. Преобразуем
эту последовательность в координаты первого узла искомой сетки по формулам
![]() ,
, ![]() .
.
Аналогично преобразуем последовательность случайных чисел ![]() , равномерно
расположенных в интервале
, равномерно
расположенных в интервале ![]() , в координаты второго узла
, в координаты второго узла
![]() ,
, ![]() .
.
И т.д. до N-го узла.
Искомой сеткой является сетка с узлами, ![]() =
=![]() ,
, ![]() =
=![]() и т.д. до узла
и т.д. до узла ![]() =
=![]() .
.
4.2. В алгоритме штрафных функций используется штрафная функция
![]() , &n
bsp;
&nbs
p;
(6)
, &n
bsp;
&nbs
p;
(6)
где
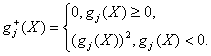 &nb
sp; &
nbsp;
(7)
&nb
sp; &
nbsp;
(7)
Задача безусловной оптимизации, к которой с помощью метода штрафных функций сводится решение исходной задачи условной оптимизации, имеет вид
![]()
![]()
![]() .
(8)
.
(8)
Если ![]() -
узлы некоторой сетки, покрывающей параллелепипед допустимых значений П, то
схема алгоритма штрафных функций можно представить в следующем виде.
-
узлы некоторой сетки, покрывающей параллелепипед допустимых значений П, то
схема алгоритма штрафных функций можно представить в следующем виде.
1)
Последовательно для ![]() в качестве начальной точки
в качестве начальной точки ![]() принимаем
узел сетки
принимаем
узел сетки ![]() и
переходим к следующему пункту.
и
переходим к следующему пункту.
2)
Если точка ![]() , то переходим к следующему пункту. Иначе -
переходим к следующей начальной точке.
, то переходим к следующему пункту. Иначе -
переходим к следующей начальной точке.
3)
Полагаем коэффициент штрафной функции ![]() =
=![]() , счетчик числа итераций
, счетчик числа итераций ![]() .
.
4)
Исходя из точки ![]() , каким-либо методом локальной безусловной
оптимизации решаем задачу (8) – находим точку
, каким-либо методом локальной безусловной
оптимизации решаем задачу (8) – находим точку ![]() .
.
5)
Проверяем условие окончания поиска (см. ниже). Если условие окончания
поиска выполнено, то в качестве решения задачи принимаем точку ![]() =
=![]() и переходим к
следующей начальной точке. Иначе – полагаем
и переходим к
следующей начальной точке. Иначе – полагаем ![]() ,
, ![]() и переходим к п. 4.
и переходим к п. 4.
6) Находим
![]() &nb
sp;
(9)
&nb
sp;
(9)
и принимаем в качестве решения задачи вектор ![]() и соответствующее значение
минимизируемой функции
и соответствующее значение
минимизируемой функции ![]() .
.
В качестве условия окончания итераций используется условие
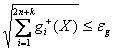 , &n
bsp;
&nbs
p;
(10)
, &n
bsp;
&nbs
p;
(10)
где ![]() -
требуемая точность выполнения ограничений (7).
-
требуемая точность выполнения ограничений (7).
4.3. Метод Нелдера-Мида является развитием симплекс-метода и использует в процессе поиска деформацию (изменение размеров и формы) текущего симплекса (не обязательно регулярного).
Регулярным симплексом в пространстве ![]() называется
правильный многогранник, образованный
называется
правильный многогранник, образованный![]() -ой равноотстоящими друг от друга
вершинами. Для случая n=2 – это равносторонний
треугольник, для случая n=3 – тетраэдр.
-ой равноотстоящими друг от друга
вершинами. Для случая n=2 – это равносторонний
треугольник, для случая n=3 – тетраэдр.
Если в пространстве ![]() необходимо построить регулярный
симплекс, одна из вершин которого находится в точке
необходимо построить регулярный
симплекс, одна из вершин которого находится в точке ![]() , то координаты вершин
такого симплекса удобно задавать с помощью
, то координаты вершин
такого симплекса удобно задавать с помощью ![]() матрицы:
матрицы:
 . &n
bsp;
. &n
bsp;
Здесь i-й столбец представляет собой
координаты i-й вершины симплекса, ![]() ;
;
![]() ,
, ![]() ; &n
bsp;
; &n
bsp;
где l – длина ребра симплекса.
Например, регулярный симплекс в двумерном пространстве ![]() с одной
из вершин в начале координат (когда
с одной
из вершин в начале координат (когда ![]() ) определяется (2*3) матрицей
) определяется (2*3) матрицей
![]()
![]()
![]()
и имеет вид, представленный на Рис. 1.
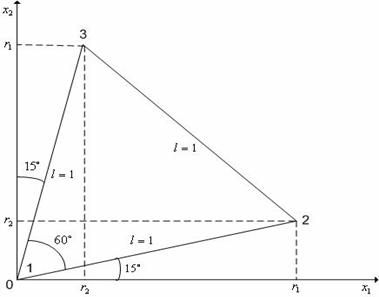
Рис. 1. Регулярный симплекс в пространстве ![]() с одной из вершин
в начале координат.
с одной из вершин
в начале координат.
Метод использует следующие операции над симплексами:
· &nb sp; отражение;
· &nb sp; редукция;
· &nb sp; сжатие;
· &nb sp; растяжение.
Отражение вершины симплекса относительно центра тяжести
остальных вершин. В результате отражения k-й
вершины симплекса с координатами вершин ![]() , получаем новый симплекс с координатами
вершин
, получаем новый симплекс с координатами
вершин
![]() ;
; ![]() , &n
bsp;
(11)
, &n
bsp;
(11)
где
![]() -
&nbs
p; &n
bsp;
(12)
-
&nbs
p; &n
bsp;
(12)
вектор координат центра тяжести остальных вершин симплекса (за исключением отраженной вершины k).
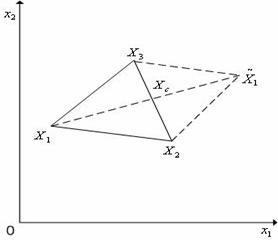
Рис. 2. Отражение вершины ![]() симплекса в пространстве
симплекса в пространстве ![]() относительно
центра тяжести
относительно
центра тяжести ![]() остальных вершин.
остальных вершин.
Редукции симплекса - уменьшение длин всех ребер симплекса в
одно и то же количество раз. В результате выполнения редукции вершин симплекса ![]() к
вершине
к
вершине ![]() получаем
новый симплекс с координатами вершин
получаем
новый симплекс с координатами вершин
![]() ,
, ![]() , &n
bsp;
(13)
, &n
bsp;
(13)
где ![]() -
коэффициент редукции.
-
коэффициент редукции.
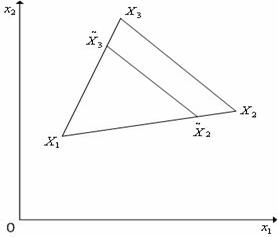
Рис. 3. Редукция вершин симплекса в пространстве ![]() к вершине
к вершине
![]() .
.
Сжатие симплекса. В результате выполнения сжатия симплекса ![]() в
направлении
в
направлении ![]() получаем
новый симплекс с координатами вершин
получаем
новый симплекс с координатами вершин
![]()
![]() &nb
sp;
(14)
&nb
sp;
(14)
где ![]() -
коэффициент сжатия,
-
коэффициент сжатия, ![]() - вектор координат центра тяжести
остальных вершин симплекса.
- вектор координат центра тяжести
остальных вершин симплекса.
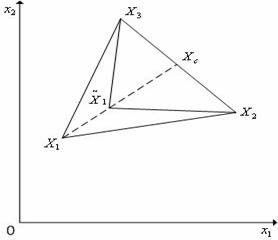
Рис. 4. Сжатие симплекса в пространстве ![]() в направлении
в направлении ![]() .
.
Растяжение симплекса. В результате выполнения растяжения симплекса
![]() в
направлении
в
направлении ![]() получаем
новый симплекс с координатами вершин
получаем
новый симплекс с координатами вершин
![]()
![]() &nb
sp;
(15)
&nb
sp;
(15)
где ![]() -
коэффициент растяжения,
-
коэффициент растяжения, ![]() - вектор координат центра тяжести
остальных вершин симплекса (см. (12)).
- вектор координат центра тяжести
остальных вершин симплекса (см. (12)).
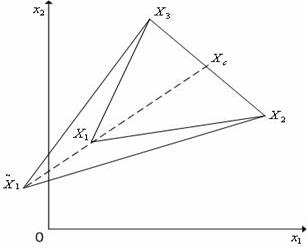
Рис. 5. Растяжение симплекса в пространстве ![]() в направлении
в направлении ![]() .
.
Схема метода Нелдера-Мида
Симплекс с вершинами ![]() обозначим
обозначим ![]() .
.
1)
Задаем начальную точку ![]() , длину ребра симплекса
, длину ребра симплекса ![]() и полагаем
и полагаем ![]() .
.
2)
Находим координаты ![]() всех вершин регулярного симплекса
всех вершин регулярного симплекса ![]() с длиной
ребра l. Вычисляем значения
с длиной
ребра l. Вычисляем значения ![]() минимизируемой
функции во всех вершинах симплекса.
минимизируемой
функции во всех вершинах симплекса.
3)
Среди вершин симплекса ![]() находим вершины
находим вершины ![]() , в которых функция
, в которых функция ![]() принимает,
соответственно, наименьшее, наибольшее и следующее за максимальным значения, а
также находим значения функции
принимает,
соответственно, наименьшее, наибольшее и следующее за максимальным значения, а
также находим значения функции ![]() в этих точках:
в этих точках:
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
4)
По формулам (11), (12) отражаем вершину ![]() относительно центра тяжести
остальных вершин симплекса – получаем новый симплекс
относительно центра тяжести
остальных вершин симплекса – получаем новый симплекс ![]() . Вычисляем значение
. Вычисляем значение ![]() минимизируемой
функции в новой вершине симплекса.
минимизируемой
функции в новой вершине симплекса.
5)
Если условие окончания итераций (см. ниже) выполнено, то в качестве приближенного
значения точки минимума функции ![]() принимаем ту вершину симплекса
принимаем ту вершину симплекса ![]() , в которой
, в которой ![]() имеет
минимальное значение, и заканчиваем вычисления.
имеет
минимальное значение, и заканчиваем вычисления.
6)
Если ![]() и
и
![]() , то
переходим к п.7 (растяжению). Если
, то
переходим к п.7 (растяжению). Если ![]() , но
, но ![]() , то переходим к п.3 (отражению).
Если
, то переходим к п.3 (отражению).
Если ![]() ,
то переходим к п.8 (сжатию).
,
то переходим к п.8 (сжатию).
7)
Ситуация ![]() и
и ![]() . По формуле (15) выполняем
растяжение симплекса
. По формуле (15) выполняем
растяжение симплекса ![]() в направлении
в направлении ![]() - получаем новый
симплекс
- получаем новый
симплекс ![]() .
Вычисляем значение минимизируемой функции в новой вершине симплекса
.
Вычисляем значение минимизируемой функции в новой вершине симплекса ![]() . Если
. Если ![]() , то полагаем
, то полагаем ![]() и
переходим к п.3 (отражению). Иначе полагаем
и
переходим к п.3 (отражению). Иначе полагаем ![]() и переходим к п.3
(отражению) с симплексом
и переходим к п.3
(отражению) с симплексом ![]() (т.е. не используем результаты
растяжения).
(т.е. не используем результаты
растяжения).
8)
Ситуация ![]() . По формуле (14) выполняем сжатие
симплекса
. По формуле (14) выполняем сжатие
симплекса ![]() в
направлении
в
направлении ![]() -
получаем новый симплекс
-
получаем новый симплекс ![]() . Вычисляем значение минимизируемой функции
в новой вершине симплекс
. Вычисляем значение минимизируемой функции
в новой вершине симплекс ![]() . Если
. Если ![]() , то полагаем
, то полагаем ![]() и переходим к п.4
(отражению). Иначе по формуле (13) выполняем редукцию симплекса
и переходим к п.4
(отражению). Иначе по формуле (13) выполняем редукцию симплекса ![]() к вершине
к вершине![]() - получаем
новый симплекс
- получаем
новый симплекс ![]() . Вычисляем значение минимизируемой функции
во всех новых вершинах симплекса
. Вычисляем значение минимизируемой функции
во всех новых вершинах симплекса ![]() . Полагаем
. Полагаем ![]() и переходим к п.3
(отражению).
и переходим к п.3
(отражению).
В качестве условия окончания итераций в методе Нелдера-Мида используется условие
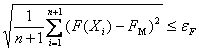 ,
,
где ![]() -
среднее значение минимизируемой функции
-
среднее значение минимизируемой функции ![]() в вершинах симплекса,
в вершинах симплекса, ![]() -
требуемая точность решения по
-
требуемая точность решения по![]() .
.
Метод Нелдера-Мида не содержит формальных правил выбора начальной точки ![]() и длины
ребра симплекса
и длины
ребра симплекса ![]() .
.
Если какая-либо информация о расположении точки минимума функции ![]() отсутствует,
то в качестве точки
отсутствует,
то в качестве точки ![]() можно взять любую точку. Если имеется
априорная информация о возможном расположении точки минимума функции
можно взять любую точку. Если имеется
априорная информация о возможном расположении точки минимума функции ![]() , то точку
, то точку ![]() следует
взять вблизи этой точки.
следует
взять вблизи этой точки.
Начальную длину ребра симплекса ![]() можно назначать, исходя из требуемой
точности решения по X, исходя из константы
Липшица минимизируемой функции
можно назначать, исходя из требуемой
точности решения по X, исходя из константы
Липшица минимизируемой функции ![]() (если она известна).
(если она известна).
5. Основные программные единицы модуля
5.1. Функция Main_MinMax_seq предназначена для нахождения минимумов и/или максимумов всех или заданных пользователем частных критериев оптимальности. Программа базируется на программе Fine1_seq.
Ниже представлена схема программы Main_MinMax_seq.
1) Создаем новый эксперимент (прежде пользователем должно быть создано соответствующее исследование).
2) Вызываем программу Experiment_Create - определяем атрибуты эксперимента. В случае неудачного завершения работы этой программы прекращаем работу.
3) Получаем все необходимые данные из БД.
4) Вызываем программу Model_Test - выполняем проверки атрибутов модели. В случае неудачного завершения работы этой программы прекращаем вычисления.
5) Вызываем программу F_information и предъявляем пользователю текущую информацию обо всех частных критериях оптимальности.
6) Предоставляем пользователю возможность задать количество частных критериев оптимальности и указать признак для каждого критерия, который определяет минимум или максимум необходимо найти.
7) Предоставляем пользователю возможность для каждого из частных критериев задать перечисленные ниже величины и выполнить проверку на их допустимость:
·
максимальное число итераций при поиске программой Nelder_Mead минимума критерия ![]() ;
;
·
требуемая точность вычисления минимума критерия ![]() ;
;
·
начальное значение коэффициента штрафа для поиска минимума критерия ![]() ;
;
·
максимально допустимое значение коэффициента штрафа для поиска минимума
критерия ![]() ;
;
· количество узлов случайной сетки по каждому из n измерений при поиске минимума частного критерия оптимальности с номером i ;
·
максимально допустимое количество вычислений
значения критерия ![]() при однократном выполнении программы Nelder_Mead.
при однократном выполнении программы Nelder_Mead.
8) Если для одного или нескольких критериев, которые задал пользователь, соответствующие экстремальные значения не вычислены (а, значит, неизвестны и средние вычислительные сложности этих критериев, а также средние значения количества итераций), то система формирует следующее сообщение «Вычислительные сложности критериев <список критериев> неизвестны. Поэтому система не может оценить время решения. Если Вы оцениваете вычислительную сложность одного или нескольких указанных критериев как высокую, то рекомендуем Вам задать небольшие максимально допустимые соответствующие количества вычислений значения критерия».
9) Последовательно для каждого из заданных пользователем частных критериев оптимальности выполняем следующие действия:
· обращаемся к программе Fine1_seq;
·
если ни одна из точек построенной случайной сетки не оказалась в области
допустимых значений, то формируем сообщение: «Отыскать минимум критерия
<номер критерия> не удалось - ни одна из начальных точек X0 не принадлежит множеству ![]() » или «Отыскать максимум критерия
<номер критерия> не удалось - ни одна из начальных точек X0 не принадлежит множеству
» или «Отыскать максимум критерия
<номер критерия> не удалось - ни одна из начальных точек X0 не принадлежит множеству ![]() »;
»;
· записываем результаты вычисления в БД;
· формируем дату конца эксперимента как текущий год, месяц, день и время;
· заканчиваем вычисления.
5.2. Функция Experiment_Create обеспечивает задание значений атрибутов эксперимента при его создании.
Схема программы:
1) Пользователь вводит с клавиатуры краткое наименование эксперимента.
2) Пользователь вводит с клавиатуры полное наименование эксперимента.
3) Пользователь вводит с клавиатуры комментарий.
4) Система формирует дату начала эксперимента как текущий год, месяц, день и время.
5.3. Функция Model_Test предназначена для проверки возможности использования выбранной пользователем метапрограммы для исследования выбранной им ранее модели.
Схема программы:
1)
Размерность вектора варьируемых параметров модели n не должна превышать максимально допустимую размерность
этого вектора ![]() , указанную в атрибутах программы. Если это
требование не выполнено, то система формирует соответствующее сообщение и не
позволяет начать эксперимент.
, указанную в атрибутах программы. Если это
требование не выполнено, то система формирует соответствующее сообщение и не
позволяет начать эксперимент.
2)
Размерность вектора частных критериев оптимальности модели m не должна превышать максимально
допустимую размерность этого вектора ![]() , указанную в атрибутах программы. Если это
требование не выполнено, то система формирует соответствующее сообщение и не
позволяет начать эксперимент.
, указанную в атрибутах программы. Если это
требование не выполнено, то система формирует соответствующее сообщение и не
позволяет начать эксперимент.
3)
Если в атрибутах модели задано, что множество ![]() принадлежит классу
множеств
принадлежит классу
множеств ![]() ,
то этот класс должен совпадать или быть подклассом класса множества
,
то этот класс должен совпадать или быть подклассом класса множества ![]() , указанного в
соответствующем атрибуте программы. Если это требование не выполнено, то
система формирует соответствующее сообщение и запрашивает у пользователя
разрешение начать эксперимент.
, указанного в
соответствующем атрибуте программы. Если это требование не выполнено, то
система формирует соответствующее сообщение и запрашивает у пользователя
разрешение начать эксперимент.
4)
Класс функций вектора частных критериев ![]() , заданный в атрибутах модели,
должен совпадать или быть подклассом класса функций
, заданный в атрибутах модели,
должен совпадать или быть подклассом класса функций ![]() , указанного в атрибутах
программы. Если это требование не выполнено, то система формирует
соответствующее сообщение и запрашивает у пользователя разрешение начать
эксперимент.
, указанного в атрибутах
программы. Если это требование не выполнено, то система формирует
соответствующее сообщение и запрашивает у пользователя разрешение начать
эксперимент.
5.4. Функция F_information предназначена для вывода на экран текущей информации обо всех частных критериях оптимальности.
5.5. Функция Fine1_seq предназначена для нахождения экстремумов частных критериев оптимальности. Ограничения в программе учитываются с помощью алгоритма штрафных функций. Для решения задачи глобальной безусловной оптимизации программа использует последовательную программу Нелдера-Мида и случайную сетку. Программа может использоваться для отыскания как локальных, так и глобальных экстремумов частных критериев.
Схема программы:
1) &nb
sp;
Устанавливаем в исходное состояние счетчики суммарного количества
вычислений частного критерия оптимальности, суммарного количества итераций в
программе, суммарного количества начальных точек, исходя из которых, фактически
выполнен поиск минимума или максимума критерия![]() .
.
2) &nb sp; Вызываем программу Random_Mesh – получаем массив, содержащий для каждого из узлов случайной сетки его n координат.
3) &nb sp; С помощью таймера фиксируем время начала вычислений.
4) &nb sp; Последовательно для каждого из узлов построенной сетки, выполняем следующие действия:
4.1) &nb sp; Вызываем программу Boundaries.
4.2) &nb sp; Если координаты данной точки не принадлежит множеству допустимых значений, то переходим к следующему узлу сетки. В противном случае переходим к следующему пункту.
4.3) &nb sp; Вызываем программу Nelder_Mead.
4.4) &nb
sp;
Если программа Nelder_Mead обеспечила вычисление экстремума критерия ![]() с
заданной точностью, то переходим к пункту 4.6).
с
заданной точностью, то переходим к пункту 4.6).
4.5) &nb
sp;
Если программа Nelder_Mead не обеспечила вычисление экстремума критерия ![]() с
заданной точностью, то увеличиваем значение штрафа в 2 раза и выполняем
следующие действия:
с
заданной точностью, то увеличиваем значение штрафа в 2 раза и выполняем
следующие действия:
· &nb sp; если еще не достигнуто максимально допустимое значение коэффициента штрафа при вычислении экстремума соответствующего частного критерия, то переходим к п. 4.3).
· &nb sp; иначе переходим к п. 5).
4.6) Вызываем функцию F_functions. В результате получаем значение экстремума частного критерия оптимальности в найденной программной Nelder_Mead точке экстремума этого критерия.
4.7)
Если заданная точность вычисления экстремума критерия ![]() обеспечена
первый раз, то происходит сохранение результатов поиска экстремума данного
критерия.
обеспечена
первый раз, то происходит сохранение результатов поиска экстремума данного
критерия.
4.8) Если имеет место не первое сохранение результатов, то выполняем следующие действия.
· &nb
sp;
если существуют результаты вычислений, соответствующие лучшему значению
критерия ![]() ,
чем полученные исходя из данного узла сетки, то переходим к следующему узлу;
,
чем полученные исходя из данного узла сетки, то переходим к следующему узлу;
· &nb sp; в противном случае, сохраняем полученное значение и переходим к следующему узлу.
5) &nb sp; Если ни одна из точек построенной случайной сетки не оказалась в области допустимых значений, то заканчиваем вычисления. В противном случае – переходим к п.6.
6) &nb sp; Выполняем следующие действия:
6.1) С помощью таймера фиксируем время окончания вычислений.
6.2) Вычисляем и сохраняем в БД следующие величины:
·
суммарное количество вычислений критерия ![]() , на основе которого определена
его средняя вычислительная сложность;
, на основе которого определена
его средняя вычислительная сложность;
·
среднюю вычислительную сложность критерия ![]() ;
;
· суммарное количество итераций в программе Nelder_Mead, на основе которого вычислено среднее количество итераций алгоритма Нелдера-Мида;
·
среднее количество итераций алгоритма Нелдера-Мида, необходимых для
отыскания экстремума критерия ![]() .
.
5.6. Вспомогательная функция Random_mesh служит для генерации случайной сетки в параллелепипеде допустимых значений П:
![]() .
.
5.7. Вспомогательная функция
Boundaries предназначена для проверки принадлежности заданного вектора X множеству допустимых значений ![]() .
.
Схема программы имеет следующий вид:
1) &nb sp; Полагаем In=1.
2) &nb sp; Вызываем функцию G_functions – вычисляем значения ограничивающих функций в точке X;
3) &nb
sp;
Для каждой ограничивающей функции проверяем условие ![]() . Если
. Если ![]() , то полагаем In=0.
, то полагаем In=0.
5.8. Функция G_functions предназначена
для вычисления значений ограничивающих функций ![]() ,
, ![]() , в узлах указанной выше сетки.
, в узлах указанной выше сетки.
5.9. Функция Nelder_Mead предназначена для решения однокритериальной безусловной задачи локальной оптимизации методом Нелдера-Мида.
Спецификация программы Nelder_Mead
Входные данные:
1)
n - размерность вектора варьируемых параметров (![]() );
);
2) alfa - параметр отражения при
построении многогранника, рекомендуемое значение: ![]() ,
,
![]() ;
;
3) beta - параметр сжатия при
построении многогранника, рекомендуемое значение:![]() ,
, ![]() ;
;
4) gam - параметр растяжения при построении многогранника,
рекомендуемое значение: ![]() ,
, ![]() ;
;
5) itmax - максимально допустимое число итераций алгоритма;
6) acc - требуемая точность вычисления
минимума критерия оптимальности (![]() );
);
7) l – исходное расстояние между двумя ближайшими вершинами симплекса (l>0);
8) X[n] - начальная точка;
9) ff – минимальное или максимальное вычисленное программой значение соответствующего критерия;
10)maxk – максимально допустимое количество вычислений значения критерия оптимальности;
11) fun - имя подпрограммы, вычисляющей значения минимизируемого критерия оптимальности;
Выходные данные:
1) itmax - фактически выполненное число итераций;
2) acc - достигнутая точность вычисления минимума критерия оптимальности;
3) X[n] - точка с минимальным вычисленным значением критерия оптимальности;
4) maxk – фактически выполненное количество вычислений критерия оптимальности;
5) ierr – признак окончания программы:
ierr = 1 - минимум найден с заданной точностью;
ierr = -1 - минимум не найден с заданной точностью, выполнено itmax итераций;
ierr = -2 - минимум не найден с заданной точностью, выполнено maxk вычислений критерия оптимальности.
Спецификация подпрограммы fun
1) n - размерность вектора параметров X;
2) X[n] – значения компонент вектора X, при которых необходимо вычислить значения частных критериев;
3) fc – вычисленное программой значение соответствующего критерия;
5.10. Функция Qunct1 предназначена для использования с функцией Nelder_Mead в качестве программы fun случае, когда необходимо найти экстремум одного из частных критериев оптимальности.
5.11. Функция F_functions вычисляет значения заданных частных критериев оптимальности.
6. Заключение
Для тестирования программы Fine1_seq рассмотрена следующая задача:
![]() ,
, ![]()
![]() - точное решение:
- точное решение: ![]() .
.
При тестировании получены следующие результаты:
1. Первый узел: ![]() , In = 1, ff = 10.000000;
, In = 1, ff = 10.000000;
2. Второй узел: ![]() , In = 0;
, In = 0;
3. Третий узел: ![]() , In = 1, ff = 10.000000;
, In = 1, ff = 10.000000;
4. Четвертый
узел: ![]() ,
In = 0.
,
In = 0.
Таким образом,
найден ![]() с
точностью до
с
точностью до ![]() .
.
Литература
1. Карпенко А.П., Федорук В.Г. Обзор программных систем многокритериальной оптимизации. Отечественные системы // Информационные технологии, ╧1, 2006, с. 15-22.
2. Карпенко А.П., Федорук В.Г. Организация последовательно-параллельной обучающей системы многокритериальной оптимизации «Парето» //Материалы Всероссийской научной конференции, посвященной 75-летию Казанского Государственного технического Университета им. А.Н.Туполева «Информационные технологии в науке, образовании и производстве», Казань, 2007, с. 618 – 620.
Публикации с ключевыми словами: многокритериальная оптимизация
Публикации со словами: многокритериальная оптимизация
Смотри также:
- Информационная модель и основные функции программной системы многокритериальной оптимизации ╚Парето╩
- Адаптивные методы решения задачи многокритериальной оптимизации, использующие аппроксимацию функции предпочтений лица, принимающего решения
- Исследование погрешности аппроксимации многомерной функции с помощью нейронных сетей с радиальными базисными функциями
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



