научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 7, июль 2008
Абакаров А.Ш., Сушков Ю.А.
Санкт-Петербургский государственный университет
г. Санкт-Петербург
Введение
В настоящее время повышается необходимость в принятии рациональных решений, как для организаций различного типа, так и для отдельно взятых индивидов. Средства, которые могут использоваться при этом, варьируются от обычной интуиции до привлечения группы высококвалифицированных экспертов, а также — применения соответствующих методов принятия решений и базирующихся на них программных систем поддержки принятия решений.
В этой статье, на базе специально разработанных авторами двух программных диалоговых систем, описывается двухэтапный подход, позволяющий произвести многокритериальный отбор рациональных (перспективных) альтернатив на конечном множестве исходных альтернатив. Основная идея подхода заключается в последовательном применении к исходному множеству многокритериальных альтернатив табличного метода (ТМ) [1] и широко известного Метода Анализа Иерархий (МАИ) [2].
Табличный метод позволяет сузить исходное множество альтернатив до некоторого небольшого множества альтернатив (например, содержащего не более семи альтернатив) , а с помощью МАИ осуществляется окончательный отбор приемлемых альтернатив на уже полученном ранее сокращенном их множестве. Используемые в этом процессе две диалоговые программные системы: “TCHOICE”, реализующая табличный метод, и “MPRIORITY” [3,4], реализующая МАИ, позволяют не только в какой-то мере автоматизировать весь процесс отбора, но и увеличивают эффективность отдельно взятых используемых методов за счет специально адаптированных под особенности методов диалоговых средств. Принципы работы с двумя программными системами в статье достаточно подробно описаны на конкретных примерах.
Основные определения
Пусть ![]() — функции, определенные
на множестве допустимых решений
— функции, определенные
на множестве допустимых решений ![]() , и являющиеся частными критериями, с
помощью которых оцениваются альтернативы из
, и являющиеся частными критериями, с
помощью которых оцениваются альтернативы из ![]() .
.
Сформируем
из частных критериев векторный критерий: ![]() . Таким образом, каждое решение
(альтернатива)
. Таким образом, каждое решение
(альтернатива)![]() характеризуется своей векторной оценкой
характеризуется своей векторной оценкой ![]() .
.
Пусть ![]() — множество всех
возможных векторов
— множество всех
возможных векторов ![]() ,
образующих
,
образующих ![]() -мерное
критериальное пространство
-мерное
критериальное пространство ![]() , каждой точке
, каждой точке ![]() которого соответствует точка критериального
пространства
которого соответствует точка критериального
пространства ![]() с
декартовыми координатами
с
декартовыми координатами ![]() .
.
Тогда задачу многокритериальной оптимизации можно записать [5] в общем виде следующим образом:
![]() (1)
(1)
Задача
Лица Принимающего Решение (ЛПР) заключается в нахождении такого вектора ![]() , который, по его мнению,
осуществляет разумный компромисс между различными критериями, по которым
производится отбор оптимальной альтернативы. Если для задачи (1) существует
такой вектор
, который, по его мнению,
осуществляет разумный компромисс между различными критериями, по которым
производится отбор оптимальной альтернативы. Если для задачи (1) существует
такой вектор ![]() ,
что
,
что ![]()
![]() , т.е. вектор,
доставляющего оптимум одновременно по всем имеющимся частным критериям, то
соответствующую альтернативу легко найти, решив соответствующую задачу
оптимизации (например, методом адаптивного случайного поиска [6,7]) — и на этом
процесс решения многокритериальной задачи может быть завершён. В практических
задачах очень важно то, что при многокритериальном выборе проявляется
противоречивость их частных критериев. Другими словами, некоторое улучшение
основной задачи по одному критерию влечет за собой определенное ухудшение по
другому критерию.
, т.е. вектор,
доставляющего оптимум одновременно по всем имеющимся частным критериям, то
соответствующую альтернативу легко найти, решив соответствующую задачу
оптимизации (например, методом адаптивного случайного поиска [6,7]) — и на этом
процесс решения многокритериальной задачи может быть завершён. В практических
задачах очень важно то, что при многокритериальном выборе проявляется
противоречивость их частных критериев. Другими словами, некоторое улучшение
основной задачи по одному критерию влечет за собой определенное ухудшение по
другому критерию.
Для
сравнения двух альтернатив по какому-либо из критериев, ЛПР вводится отношение
бинарного предпочтения, т.е., для любых двух альтернатив ![]() и критерия
и критерия ![]() существуют только три возможных
варианта: либо альтернатива
существуют только три возможных
варианта: либо альтернатива ![]() лучше альтернативы
лучше альтернативы ![]() (обозначим как
(обозначим как ![]() , либо альтернатива
, либо альтернатива ![]() хуже альтернативы
хуже альтернативы![]() , обозначим как
, обозначим как ![]() , либо альтернативы
равноценны, т.е.
, либо альтернативы
равноценны, т.е. ![]() .
Вводимое ЛПР отношение бинарного предпочтения характеризует его мнение,
предпочтения, пожелания и т.п. [9]
.
Вводимое ЛПР отношение бинарного предпочтения характеризует его мнение,
предпочтения, пожелания и т.п. [9]
Известный
принцип Парето [5] гласит, что выбор следует проводить не на всем множестве
возможных решений ![]() ,
а на некотором его подмножестве
,
а на некотором его подмножестве ![]() , называемом в литературе множеством
недоминируемных решений, или множеством парето-оптимальных альтернатив.
Множество Парето можно определить следующим способом:
, называемом в литературе множеством
недоминируемных решений, или множеством парето-оптимальных альтернатив.
Множество Парето можно определить следующим способом:
![]() .
.
Именно для множества Парето справедливо утверждение о том, что улучшение итогового решения по одному из критериев влечет за собой ухудшение по другому или другим критериям, поэтому множество Парето называют еще и множеством неулучшаемых альтернатив.
Множество
всех векторов ![]() называют
парето-оптимальными векторами. Для нахождения парето-оптимальных альтернатив
можно воспользоваться подходом, также базирующимся на адаптивном случайном
поиске и специальных функциях, зависящих от частных критериев и некоторого
вектора параметров [8].
называют
парето-оптимальными векторами. Для нахождения парето-оптимальных альтернатив
можно воспользоваться подходом, также базирующимся на адаптивном случайном
поиске и специальных функциях, зависящих от частных критериев и некоторого
вектора параметров [8].
Табличный метод
Основная идея табличного метода заключается в представлении исходных данных (оптимальных по Парето) в виде таблицы, где столбцы соответствуют критериям, по которым принимается решение, а строки — альтернативам (назовем эту таблицу рабочей), с последующей сортировкой ЛПР значений каждого столбца и назначением такой границы для каждого из критериев, выход за которую, по мнению ЛПР, является недопустимым. Все альтернативы не выходящие за установленную границу считаются приемлемыми (приемлемые альтернативы будем называть перспективным множеством решений). Если, по мнению ЛПР, количество таких альтернатив велико, уже имеющуюся границу можно ужесточить, например, начав с наиболее значимого критерия. Таким образом, задача ЛПР состоит в таком выборе границы, при которой, с одной стороны перспективное множество не было бы пустым, а с другой — было бы не слишком большим по мощности. Этот выбор при исследовании рабочей таблицы он делает, исходя из своего опыта, профессионализма и интуиции [1].
Пусть Парето-оптимальные альтернативы перенумерованы числами
от 1 до ![]() и
пусть
и
пусть ![]() равно
значению
равно
значению ![]() -го
критерия в
-го
критерия в ![]() -й
точке ,
-й
точке , ![]() ,
, ![]() . Эти значения критериев
определяют матрицу
. Эти значения критериев
определяют матрицу![]() .
.
Пусть ![]() — перестановка на
множестве альтернатив 1 : p порожденная ранжированием
— перестановка на
множестве альтернатив 1 : p порожденная ранжированием ![]() -го столбца матрицы
-го столбца матрицы ![]() . Базируясь на отношении строгого предпочтения, введенное
ЛПР, упорядочим элементы каждого столбца в порядке уменьшения своей
значимости. Получим рабочую таблицу, в которой на месте пересечения
. Базируясь на отношении строгого предпочтения, введенное
ЛПР, упорядочим элементы каждого столбца в порядке уменьшения своей
значимости. Получим рабочую таблицу, в которой на месте пересечения ![]() -ой строки и
-ой строки и ![]() -го столбца стоит элемент
-го столбца стоит элемент
![]() .
Рабочая таблица является основным объектом, с которым работает ЛПР в диалоге с
компьютером.
.
Рабочая таблица является основным объектом, с которым работает ЛПР в диалоге с
компьютером.
Пусть ![]() означает самое худшее
значение критерия, хуже которого, по мнению ЛПР, на данном этапе диалога этот
критерий принимать не может. Вектор
означает самое худшее
значение критерия, хуже которого, по мнению ЛПР, на данном этапе диалога этот
критерий принимать не может. Вектор ![]() назовем границей.
назовем границей.
Пусть ![]() — множество
альтернатив, удовлетворяющих введенному ограничению по
— множество
альтернатив, удовлетворяющих введенному ограничению по![]() -му критерию. Тогда
множество
-му критерию. Тогда
множество
![]()
является перспективным множеством альтернатив.
Задача
ЛПР состоит в таком выборе границы ![]() , при котором, с одной стороны, перспективное
множество не было бы пустым, а с другой — было бы не слишком большим по мощности,
c тем, чтобы в дальнейшем для выбора из полученного множества
альтернатив было проще использовать метод МАИ. Этот выбор при исследовании
рабочей таблицы он делает, исходя из своего опыта, профессионализма и интуиции.
, при котором, с одной стороны, перспективное
множество не было бы пустым, а с другой — было бы не слишком большим по мощности,
c тем, чтобы в дальнейшем для выбора из полученного множества
альтернатив было проще использовать метод МАИ. Этот выбор при исследовании
рабочей таблицы он делает, исходя из своего опыта, профессионализма и интуиции.
В связи с этим
ЛПР может вновь вернуться к рабочей таблице и изменить границу в сторону
увеличения значимости критериев (какие именно при этом будут выбраны критерии,
зависит от ЛПР и решаемой им задачи). Возможна и обратная картина, т.е. граница
![]() уже с самого
начала оказывается такой жесткой, что множество перспективных решений является
пустым. В этом случае необходимо изменить границу
уже с самого
начала оказывается такой жесткой, что множество перспективных решений является
пустым. В этом случае необходимо изменить границу ![]() в сторону уменьшения значимости критериев.
в сторону уменьшения значимости критериев.
Повторяя неоднократно процедуру установки границы, в конечном счете, можно получить перспективное множество с необходимым количеством альтернатив, каждая альтернатива будет определять вариант решения многокритериальной задачи.
Разберем работу табличного метода на примере упрощенной задачи выбора автомобиля. Воспользуемся данными, представленными в таблице 1.
Таблица 1.
|
Номер альтернативы |
Наименование критерия |
||
|
Стоимость (тыс. у.е.) |
Расход топлива (литр) |
Марка |
|
|
1 |
25 |
10 |
Мерседес |
|
2 |
15 |
9 |
БМВ |
|
3 |
12 |
8 |
Форд |
|
4 |
9 |
7 |
КИА |
|
5 |
8 |
7 |
ВАЗ |
Упорядочим альтернативы по каждому из критериев в порядке уменьшения своей значимости для ЛПР. Предположим, что альтернативы были отсортированы следующим образом (таблица 2).
Таблица 2.
Наименование критерия |
||
|
Стоимость |
Расход топлива |
Марка |
|
8 |
7 |
Мерседес |
|
9 |
7 |
БМВ |
|
12 |
9 |
КИА |
|
15 |
8 |
Форд |
|
25 |
10 |
ВАЗ |
Выделим из исходного множества множество парето-оптимальных альтернатив. Альтернатива, соответствующая автомобилю марки КИА, доминирует над альтернативой, соответствующей автомобилю марки Форд. Таким образом, парето-оптимальное множество, среди которого следует производить дальнейший выбор, состоит из четырех перспективных альтернатив (таблица 3).
Таблица 3.
Наименование критерия |
||
|
Стоимость |
Расход топлива |
Марка |
|
8 |
7 |
Мерседес |
|
9 |
7 |
БМВ |
|
15 |
9 |
КИА |
|
25 |
10 |
ВАЗ |
Автомобиль ВАЗ остается недоминируемой альтернативой, т.к., несмотря на свое последнее место в третьем столбце, автомобиль ВАЗ самый дешевый, а значит, должен занять первое место в первом столбце.
Данные,
представленные в таблице 3, именуются рабочей таблицей. Следующим шаг —
установка границы. Предположим, что ЛПР готов заплатить за свой новый
автомобиль не более 18 тыс. у.е., т.е., ![]() . Для обозначения этого факта наглядно,
воспользуемся двумя цветами, в желтый цвет будут окрашены альтернативы
удовлетворяющие установленным ограничениям ЛПР, красным — не удовлетворяющие(таблица
4). Расход топлива не более 9 литров считается приемлемым для ЛПР. Что касается
третьего критерия, то здесь ЛПР считает приемлемыми для него лишь заграничные
марки автомобилей. Таким образом, получаем следующую рабочую таблицу.
. Для обозначения этого факта наглядно,
воспользуемся двумя цветами, в желтый цвет будут окрашены альтернативы
удовлетворяющие установленным ограничениям ЛПР, красным — не удовлетворяющие(таблица
4). Расход топлива не более 9 литров считается приемлемым для ЛПР. Что касается
третьего критерия, то здесь ЛПР считает приемлемыми для него лишь заграничные
марки автомобилей. Таким образом, получаем следующую рабочую таблицу.
Таблица 4.
Наименование критерия |
||
|
Стоимость |
Расход топлива |
Марка |
|
8 |
7 |
Мерседес |
|
9 |
7 |
БМВ |
|
15 |
9 |
КИА |
|
25 |
10 |
ВАЗ |
Следующий шаг заключается в определении перспективного множества, соответствующего установленной границе. Такое множество представлено в таблице 5.
Таблица 5.
Наименование критерия |
||
|
Стоимость |
Расход топлива |
Марка |
|
15 |
9 |
БМВ |
|
9 |
7 |
КИА |
Текущее перспективное множество содержит два автомобиля. Предположим, что ЛПР решил уменьшить текущее перспективное множество до одного автомобиля. Для этого, как уже было сказано выше, следует ужесточить текущую границу. Пусть ЛПР решил, что его будущий автомобиль должен расходовать меньше горючего, т.е., решил ужесточить имеющееся ограничение по второму критерию (таблица 6).
Таблица 6.
Наименование критерия |
||
|
Стоимость |
Расход топлива |
Марка |
|
8 |
7 |
Мерседес |
|
9 |
7 |
БМВ |
|
15 |
9 |
КИА |
|
25 |
10 |
ВАЗ |
Ужесточая границу по второму критерию, получаем перспективное множество, состоящее из одной альтернативы, — автомобиль КИА. Ужесточение ограничения по критерию "Стоимость" приводит к аналогичному перспективному множеству.
Следует добавить, что программная система “T-CHOICE”, базирующаяся на табличном методе, дополняет последний диалоговым средством, позволяющим делать процесс корректировки текущей границы более направленным, предоставляя ЛПР информацию, облегчающую процесс корректировки текущей границы.
Диалоговая система “T-CHOICE”
Программная система "T-CHOICE" автоматизирует работу ЛПР, позволяя:
- выполнять ранжирование альтернатив в зависимости от предпочтений ЛПР,
- выделять множество Парето оптимальных альтернатив,
- устанавливать текущую границу,
- находить перспективное множество, соответствующее текущим границам, а также,
- дополняет табличный метод некоторыми диалоговыми возможностями, повышающими его эффективность.
Программная система содержит три рабочих вкладки, называемые: "Главная таблица", "Текущие альтернативы", "Отобранные альтернативы" (рис.1).
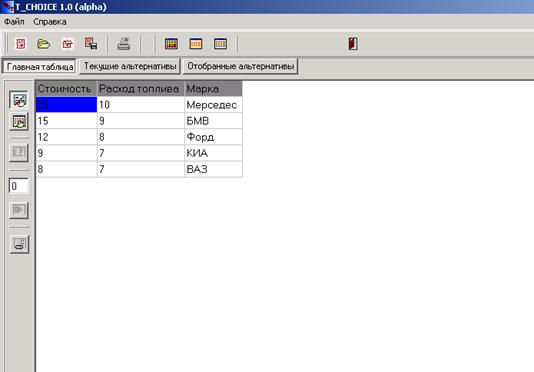
Рис. 1. Главное окно диалоговой системы “T-CHOICE”.
Закладка "Главная таблица" — позволяет ЛПР выполнить все необходимые шаги табличного метода, включая ввод и коррекцию исходных данных.
"Текущие альтернативы" — предназначена для хранения текущего перспективного множества альтернатив, полученных после установки ЛПР очередной границы. Для каждой вновь установленной границы перспективное множество, отображаемое на вкладке "Текущие альтернативы", обновляется.
"Отобранные альтернативы" — предназначена для накопления и хранения альтернатив, специально отобранных ЛПР из текущих перспективных множеств, полученных в процессе диалога (в основном, в процессе изменения текущих границ).
Основная таблица, расположенная на закладке "Главная таблица", может содержать данные следующих четырех типов:
- неопределенный,
- строковый,
- численный (вещественный),
- логический.
Данные одной колонки основной таблицы являются данными одного типа.
Введенные типы данных позволяют формализовать работу программной системы с исходными данными. Например, если пользователь установит тип данных как численный, то система сможет автоматически отсортировать данные в порядке уменьшения или увеличения значимости альтернатив. То же самое касается и логического типа, используемого для случая, когда альтернатива может принимать лишь два значения: Истина (True) и Ложь (False). Если же данные являются данными строкового типа, то здесь пользователю следует проводить сортировку данных вручную.
Коротко опишем существующие в диалоговой системе дополнения к табличному методу. На панели управления закладки "Главная таблица" находится счетчик числа альтернатив текущего перспективного множества (на рисунке 2 счетчик обозначен меткой А). После каждого изменения границы ЛПР может видеть количество альтернатив в текущем перспективном множестве.
Кнопка ![]() позволяет
ЛПР получать дополнительную информацию о текущей рабочей таблице (рис.2). После ее активации к наименованиям альтернатив
в основной таблице добавляются числа, показывающие, какое количество
альтернатив будет содержать перспективное множество, в случае, если ЛПР
установит ограничение на соответствующей ячейке. Таким образом, ЛПР будет легче
определить, по какому из критериев ему следует ужесточить или, наоборот, ослабить
текущую границу (рис.2).
позволяет
ЛПР получать дополнительную информацию о текущей рабочей таблице (рис.2). После ее активации к наименованиям альтернатив
в основной таблице добавляются числа, показывающие, какое количество
альтернатив будет содержать перспективное множество, в случае, если ЛПР
установит ограничение на соответствующей ячейке. Таким образом, ЛПР будет легче
определить, по какому из критериев ему следует ужесточить или, наоборот, ослабить
текущую границу (рис.2).
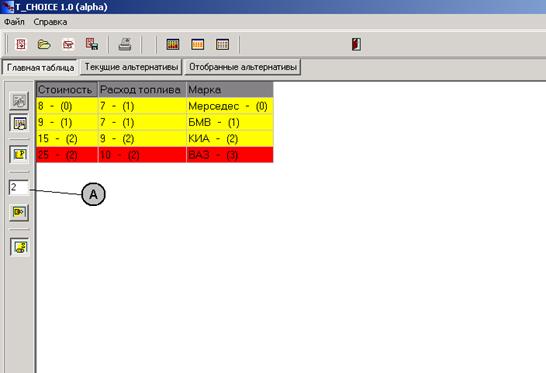
Рис. 2. Диалоговые средства “T-CHOICE”, дополняющие табличный метод.
Метод Анализа Иерархий
Метод Анализа Иерархий (МАИ) широко известен и подробно изложен во многих книгах и статьях, тем не менее, приведем здесь его краткое описание (при описании МАИ будут использоваться возможности и диалоговые окна программной системы “MPRIORITY”)
Идея МАИ была предложена в работах [2, 10, 11]. Метод анализа иерархий — эффективный и доступный нематематику метод. Основное назначение метода — решение слабоструктурированных задач принятия решений.
Известно, что в основе процесса познания человеком окружающей действительности лежат декомпозиция и синтез. При изучении какой-либо системы, человек производит ее декомпозицию на подсистемы, и затем, выявив отношения между подсистемами, производит ее синтез. Декомпозиция и синтез используются в МАИ для создания структуры задачи принятия решений (ПР) — иерархии. В вершине иерархии, используемой в МАИ для представления задачи ПР, располагается основная цель, далее, на уровень ниже — подцели, и, наконец, на самом нижнем уровне ─ альтернативы, среди которых производится выбор (и) или ранжирование. Цель, подцели, альтернативы далее будем называть объектами или элементами иерархии.
Иерархия для примера 2 представлена на (рис. 3).
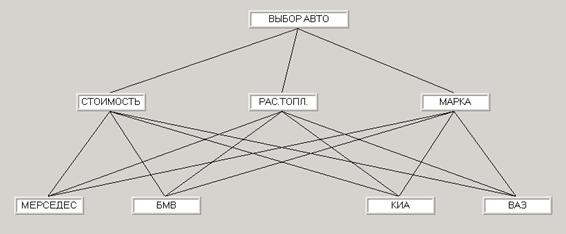
Рис.3. Пример иерархии МАИ.
В МАИ иерархия является основным способом представления структуры задачи ПР. Основное назначение иерархии в МАИ — оценка высших уровней иерархии исходя из взаимодействия ее различных уровней. Например, для иерархии на рис. 3. производится оценка ее нижнего уровня (рассматриваемые автомобили) через второй уровень (частные критерии), который в свою очередь используется для оценивания главного критерия.
Следующим этапом (этапом 2) является осуществление попарного сравнения отдельных компонент иерархии (далее просто сравнения).
Попарные сравнения — это процесс, согласно которому ЛПР сравнивает все пары объектов из некоторого списка по некоторому критерию, указывая каждый раз, более предпочитаемый объект (по этому критерию).
Все результаты попарных сравнений заносятся в соответствующую таблицу (матрицу попарных сравнений), по которой потом проводятся необходимые вычисления.
На рис. 4. представлена такая таблица (матрица попарных сравнений) для иерархии на рис. 3 (таблица расположена в центре диалогового окна “Работа эксперта”). В таблице осуществляются сравнения объектов второго уровня иерархии (рис. 3) относительно главной цели “Выбор автомобиля”. Каждая ячейка таблицы (матрицы попарных сравнений) предназначена для хранения результата сравнения двух соответствующих объектов.
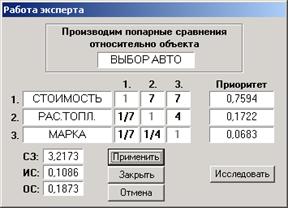
Рис. 4. Диалоговое окно с матрицей попарных сравнений.
Этап 2 позволяет ЛПР установить интенсивность взаимодействия между элементами иерархии или силу, с которой различные элементы одного уровня иерархии влияют на элементы предшествующего уровня.
Используемая в [2] качественная шкала представлена в таблице 7. Как видно из представленной шкалы, максимально возможное численное превосходство одного объекта над другим — 9. Чем обоснован верхний предел 9? Перечислим основные причины использования приведенной шкалы и верхнего предела 9:
a) качественные различия значимы на практике в том случае, когда сравниваемые объекты близки относительно критерия (свойства), использованного для сравнения;
b) способность человека проводить качественные различия между объектами можно представить пятью качественными характеристиками: равный, слабый, сильный, очень сильный и абсолютный (для достижения большей точности, вводятся компромиссные характеристики между перечисленными выше характеристиками);
c) известно [12], что оперативная память человека способна манипулировать одновременно 7 (±2) единицами информации, поэтому приведенная шкала включает в себя не более девяти градаций;
d) эффективность использования приведенной шкалы подтверждена практикой.
Таблица 7.
|
Степень важности |
Определение |
Комментарии |
|
1 |
Одинаковая важность. |
Два объекта вносят одинаковый вклад в достижение цели. |
|
3 |
Слабая значимость. |
Опыт и суждение дают легкое предпочтение одному объекту перед другим. |
|
5 |
Существенная или сильная значимость. |
Опыт и суждение дают сильное предпочтение одному объекту перед другим. |
|
7 |
Очень сильная и очевидная значимость. |
Предпочтение одного объекта перед другим очень сильно. Его превосходство практически явно. |
|
9 |
Абсолютная значимость. |
Свидетельства в пользу предпочтения одного объекта в высшей степени убедительны. |
|
2,4,6,8 |
Промежуточные значения между соседними значениями шкалы. |
Ситуации, когда необходимы компромиссные решения. |
|
Обратные величины приведенных выше значений |
Если при сравнении объекта A с объектом B мы получим одно из приведенных выше значений, то, соответственно, результат сравнения объекта B с объектом A есть обратная величина. |
|
После того, как ЛПР проведет все сравнения, по полученным данным можно вычислить соответствующий вектор приоритетов, отвечающий предпочтениям ЛПР (вектор приоритетов есть собственный вектор матрицы попарных сравнений [2,10,11]). Согласно вектору приоритетов, расположенному в правой части диалогового окна (рис. 4.), частный критерий “Стоимость” является наиболее предпочтительным для ЛПР.
Диалоговое окно качественной шкалы, используемой в программе “MPRIORITY”, представлено на рис. 5. Как видно из рис. 5, ЛПР, при сравнении объектов, использует только качественные характеристики, при этом в матрице попарных сравнений отображаются соответствующие им количественные значения.
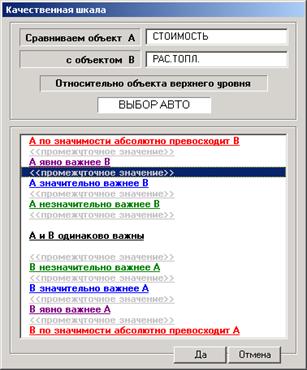
Рис. 5. Диалоговое окно качественной шкалы.
Для того чтобы полученные с помощью МАИ результаты были адекватны ситуации, в которой принимается решение, необходимо, чтобы в матрицах попарных сравнений достигалась требуемые уровни согласованности данных.
Под согласованностью матрицы попарных сравнений понимается численная (кардинальная) согласованность и транзитивная (порядковая) согласованность.
Пример кардинальной несогласованности. Пусть объект A лучше объекта B в 2 раза, а объект B лучше объекта C в 3 раза, таким образом, объект A лучше объекта C в 2x3=6 раз. Нарушение этого равенства в рамках выбранной шкалы считается кардинальной несогласованностью.
Пример
транзитивной несогласованности. Пусть объект A предпочтительнее объекта B
(обозначим как A ![]() B), а объект B
предпочтительнее объекта C (B
B), а объект B
предпочтительнее объекта C (B ![]() C),
таким образом, объект A предпочтительнее объекта C (A
C),
таким образом, объект A предпочтительнее объекта C (A ![]() C). Нарушение
последнего неравенства называется транзитивной несогласованностью.
C). Нарушение
последнего неравенства называется транзитивной несогласованностью.
Для оценки согласованности в МАИ вводятся следующие величины:
· ИС - индекс согласованности;
· ОС - отношение согласованности.
Принято считать, что для согласованных данных ОС не должно превышать 0.1 (10%), в некоторых случаях 0.2 (20%). Если ОС превышает допустимый практикой предел, то проведенные сравнения можно пересмотреть. Для улучшения согласованности в "MPRIORITY" используется соответствующий диалог.
Заметим, что совсем не обязательно добиваться того, чтобы данные было полностью согласованы (ОС = 0). Более того, оставаясь в пределах шкалы 1-9 в большинстве случаев этого добиться просто невозможно. Вполне достаточно, если согласованность суждений ЛПР будет лежать в приемлемых для практических задач границах.
Таким образом, метод МАИ включает в себя следующие четыре этапа.
Этап 1. Построение соответствующей иерархии задачи ПР (принятия решений).
Этап 2. Попарное сравнение всех элементов иерархии.
Этап 3. Устранение несогласованности матриц попарных сравнений (если это необходимо).
Этап 4. Математическая обработка полученной от ЛПР информации.
Диалоговая система “MPRIORITY”
Главное окно программы “MPRIORITY”представлено на рисунке 6.
Программа содержит диалоговые средства, позволяющие:
· работать одновременно с несколькими задачами ПР (или несколькими иерархиями одной задачи ПР) ─ "MPRIORITY" является MDI-приложением;
· строить иерархии, необходимые для задачи (для этого в системе предусмотрен режим “Редактирования”);
· проводить попарные сравнения всех объектов иерархии (для этого в системе существует режим “Работы эксперта”; порядок сравнения полностью определяется пользователем);
· получать наиболее полную информацию о текущих сравнениях;
· устранять в случае необходимости возможные несогласованности данных в матрицах попарных сравнений;
· получать вектор приоритетов не только самого нижнего уровня иерархии, но и любого выбранного пользователем уровня.
Средством, позволяющим адаптировать программную систему под конкретные области человеческой деятельности, является использование шаблонов — готовых иерархий для “стандартных” задач принятия решений. Под стандартными задачами можно понимать наиболее распространенные задачи ПР, встречающиеся в различных областях человеческой деятельности

Рис. 6. Главное окно программы “MPRIORITY”.
Двухэтапная процедура отбора перспективных альтернатив
Предлагаемый в статье подход базируется на последовательном применении к исходному множеству альтернатив табличного метода и МАИ. Основное назначение табличного метода в этом случае — сужение исходного множества альтернатив до некоторого числа наиболее перспективных альтернатив. Табличный метод позволит ЛПР справиться с этой задачей достаточно быстро. В свою очередь, Метод Анализа Иерархии, как более тонкий инструмент, должен позволить ЛПР сделать свой окончательный выбор.
Основные преимущества такого подхода состоят в следующем:
1. Позволяет увеличить мощность исходного множества альтернатив;
2. Значительно сокращает время отбора приемлемых альтернатив (прежде всего за счет уменьшения количества попарных сравнений в случае применения одного лишь МАИ). При этом качество принимаемых решений не ухудшается;
3. Позволяет ЛПР сконцентрироваться на наиболее перспективных альтернативах, полученных после применения табличного метода;
Описанные здесь программные системы значительно автоматизируют работу ЛПР, а также расширяют возможности обоих методов посредством специально разработанных диалоговых средств.
Предложенная процедура в сочетании с созданными программными системами применима в различных областях человеческой деятельности, например, при отборе персонала. В этом случае табличный метод позволит достаточно быстро отсеять наименее перспективных кандидатов, а МАИ — выбрать из оставшихся альтернатив наиболее перспективные.
Работа выполнена при финансовой поддержке грантов: Правительства Санкт-Петербурга (PD05-1.1-23) и РФФИ-ГФЕН Китая (04-01-39002ГФЕН2004_а)
Список литературы
1. Сушков Ю.А. Многокритериальность в многорежимных системах. // Архитектура и программное оснащение цифровых систем. М.: МГУ, 1984. С.71-77.
2. Саати Т. Принятие решений. Метод анализа иерархий. — М.: Радио и связь, 1993, 316 с.
3. Абакаров А.Ш., Сушков Ю.А. Программная система поддержки принятия рациональных решений “MPRIORITY 1.0” // Электронный научный журнал "Исследовано в России", 2005, стр. 2130-2146. http://zhurnal.ape.relarn.ru/articles/2005/207.p df.
4. Абакаров А.Ш., Сушков Ю.А. Программная система для выделения наилучшей альтернативы из множества имеющихся альтернатив. (MPRIORITY). Свидетельство об официальной регистрации программы для ЭВМ ╧2005612330 от 08 сентября 2005 г.
5. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. — М.: "Наука", 1982. — 254 с.
6. Сушков Ю.А. Об одном способе организации случайного поиска. // Исследование операций и статистическое моделирование. Л.: ЛГУ, 1972. С.180-185.
7. Абакаров А.Ш., Сушков Ю.А. Программа поиска оптимальных решений разной природы при заданной модели пользователя (OPTIMUM). Свидетельство об официальной регистрации программы для ЭВМ ╧2005611280 от 31 мая 2005 г.
8. Абакаров А.Ш., Сушков Ю.А. О численном подходе к получению Парето-оптимальных альтернатив // Наука в образовании: Электронное научное издание, 2008 г. http://technomag.edu.ru/doc/93468.html.
9. Ногин В.Д. Принятие решений в многокритериальной среде. Количественный подход. — М.: Физматлит, 2002. — 176 с.
10. Ушаков И.А. Задача о выборе предпочтительного объекта. // Известия АН СССР. Техническая кибернетика. 1971. ╧4. С.3-7.
11. Брук Б.Н., Бурков В.Н. Методы экспертных оценок в задачах упорядочения объектов. // Известия АН СССР. Техническая кибернетика. 1972. ╧3. С.29-39.
12. Миллер Г. Магическое число семь плюс или минус два. О некоторых пределах нашей способности перерабатывать информацию. // Инженерная психология. — М.: Прогресс, 1964, — C. 192-225.
Публикации с ключевыми словами: табличный метод, принятие решений, многокритериальная оптимизация, метод анализа иерархий
Публикации со словами: табличный метод, принятие решений, многокритериальная оптимизация, метод анализа иерархий
Смотри также:
- Исследование погрешности аппроксимации многомерной функции с помощью нейронных сетей с радиальными базисными функциями
- Информационная модель и основные функции программной системы многокритериальной оптимизации ╚Парето╩
- Разработка модуля однокритериальной оптимизации для системы многокритериальной оптимизации ╚Парето╩
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



