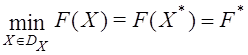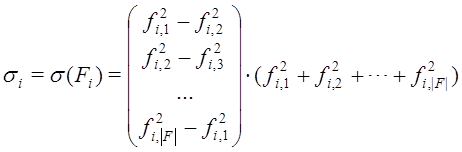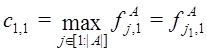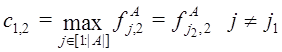научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2012
DOI: 10.7463/0412.0363023
УДК.519.6
МГТУ им. Н.Э. Баумана
mitinakaterina@gmail.com
Введение
Известно большое число методов решения задачи многокритериальной оптимизации (МКО-задачи), из числа которых перспективными являются методы, основанные на предварительном построении аппроксимации множества Парето (а тем самым, и фронта Парето) этой задачи [1, 2]. Простейшим из таких методов является сеточный метод [3]. В ситуации, когда требуется высокая точность аппроксимации множеств Парето и/или когда имеет место высокая вычислительная сложность целевых функций, сеточный метод может требовать неприемлемо высоких вычислительных ресурсов. Поэтому в настоящее время интенсивно развиваются альтернативные методы [4].
Обычно указанные методы строят на основе эволюционных алгоритмов и чаще всего – на основе генетических алгоритмов [5]. При этом соответствующие методы Парето-аппроксимации называют эволюционными. Обзор таких методов представлен, например, в работах [6, 7].
Принципиальным в этих методах является не использование именно эволюционных алгоритмов, а правила формирования фитнесс-функции, обеспечивающие перемещение индивидов популяции, в конечном счете, в направлении множества Парето. Эволюция же этих индивидов может протекать по законам, отличным от законов, используемых в эволюционных алгоритмах, например, по законам миграции частиц в алгоритме роя частиц [8, 9]. Поэтому в качестве общего названия рассматриваемых методов используем термин «популяционные методы Парето-аппроксимации».
Для полноты картины, наряду с популяционными методами в работе рассматриваем наиболее известные не популяционные методы. Особенностью обзора является то, что в той его части, которая посвящена популяционным методам, мы концентрируем наше внимание, преимущественно, на правилах формирования фитнесс-функции, используемых в этих методах.
Можно выделить следующие основные требования к методам Парето-аппроксимации [7]:
- точки найденной аппроксимации расположены достаточно близко к точному множеству Парето;
- аппроксимация покрывает все множество Парето;
- распределение точек аппроксимации равномерно.
В современных методах Парето-аппроксимации для выполнения последнего требования используют специальные механизмы, обеспечивающие приемлемый разброс (spread) точек аппроксимации. Наиболее известным механизмом такого сорта является механизм нишевания (niching) [10]. Самостоятельную проблему представляет разработка критериев оценки качества Парето-аппроксимации, которые отражали бы указанные требования. Примеры таких критериев рассмотрены, например, в работах [11, 12].
Известно несколько классификаций методов Парето-аппроксимации. Используем классификацию, предложенную Гуменниковой А. В. [13], дополнив ее классом «наивных» методов [14] и классом прочих методов. Итого рассматриваем следующие пять классов методов Парето-аппроксимации:
- «наивные» методы;
- методы переключающихся целевых функций;
- методы агрегации целевых функций;
- методы на основе ранжирования агентов популяции;
- прочие методы.
В разделе 1 приведена математическая постановка задачи, разделы 2 - 6 посвящены рассмотрению указанных классов методов Парето-аппроксимации. В заключении сформулированы основные выводы.
1. Постановка задачи и общая схема популяционных алгоритмов ее решения
Совокупность частных критериев оптимальности (частных целевых функций) ![]()
![]() образует векторный критерий оптимальности (векторную целевую функцию)
образует векторный критерий оптимальности (векторную целевую функцию) ![]() , где
, где ![]() - вектор варьируемых параметров;
- вектор варьируемых параметров; ![]() ,
, ![]() - пространства параметров и критериев соответственно. Здесь и далее запись вида
- пространства параметров и критериев соответственно. Здесь и далее запись вида ![]() , где A ─ некоторый вектор или счетное множество, означает размерность этих объектов. Положим, что ставится задача минимизации каждого из частных критериев в одной и той же области допустимых значений
, где A ─ некоторый вектор или счетное множество, означает размерность этих объектов. Положим, что ставится задача минимизации каждого из частных критериев в одной и той же области допустимых значений ![]() . Тогда во введенных обозначениях МКО-задачу условно можно записать в виде
. Тогда во введенных обозначениях МКО-задачу условно можно записать в виде
где ![]() ‑ решения задачи.
‑ решения задачи.
Полагаем, что частные критерии оптимальности нормализованы, например, по формуле
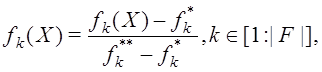
где ![]()
![]() ,
, ![]() .
.
Векторный критерий оптимальности ![]() выполняет отображение области
выполняет отображение области ![]() в некоторое множество
в некоторое множество ![]() , называемое множеством достижимости МКО-задачи (1). Введем на множестве
, называемое множеством достижимости МКО-задачи (1). Введем на множестве ![]() отношение предпочтения
отношение предпочтения ![]() . Будем говорить, что вектор
. Будем говорить, что вектор ![]() предпочтительнее вектора
предпочтительнее вектора ![]() и писать
и писать ![]() , если среди равенств и неравенств
, если среди равенств и неравенств ![]() ,
, ![]() имеется, хотя бы одно строгое неравенство. Аналогично, на множестве
имеется, хотя бы одно строгое неравенство. Аналогично, на множестве ![]() введем отношение доминирования: будем говорить, что вектор
введем отношение доминирования: будем говорить, что вектор ![]() доминирует вектор
доминирует вектор ![]() , и писать
, и писать ![]() , если
, если ![]() .
.
Выделим из множества ![]() подмножество
подмножество ![]() точек, среди которых нет доминируемых. Это множество называют фронтом Парето. Множество
точек, среди которых нет доминируемых. Это множество называют фронтом Парето. Множество ![]() , соответствующее множеству
, соответствующее множеству ![]() , называют множеством Парето (переговорным множеством, областью компромисса). Определения множества и фронта Парето иллюстрирует рисунок 1. Поскольку множество
, называют множеством Парето (переговорным множеством, областью компромисса). Определения множества и фронта Парето иллюстрирует рисунок 1. Поскольку множество ![]() на этом рисунке является выпуклым, фронт Парето
на этом рисунке является выпуклым, фронт Парето ![]() в данном случае представляет собой дугу
в данном случае представляет собой дугу ![]() , на которой точка
, на которой точка ![]() соответствует
соответствует ![]() , а точка
, а точка ![]() ─
─ ![]() . Среди точек
. Среди точек ![]() ,
, ![]() , лежащих на фронте Парето, нет доминируемых, поскольку если
, лежащих на фронте Парето, нет доминируемых, поскольку если ![]() , то обязательно
, то обязательно ![]() .
.
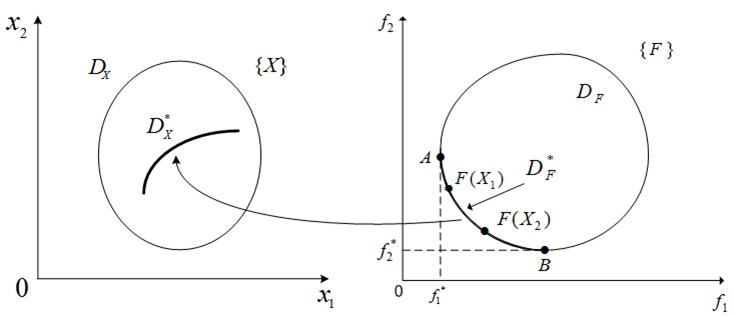
Рисунок 1 - К определению множества Парето: ![]() ;
; ![]()
Ставим задачу приближенного построения множества Парето (а, тем самым, и фронта Парето) в МКО-задаче (1). Называем эту задачу задачей Парето-аппроксимации.
Пусть тем или иным образом уже сформировано архивное множество ![]() , содержащее не доминируемые точки
, содержащее не доминируемые точки ![]() , а также архивное множество
, а также архивное множество ![]() соответствующих ему точек
соответствующих ему точек ![]() . Здесь
. Здесь ![]() - мощность множеств
- мощность множеств ![]() ,
, ![]() .
.
Суть большинства популяционных методов Парето-аппроксимации состоит в итерационном уточнении множеств точек в архивах ![]() ,
, ![]() . Если при этом на итерации
. Если при этом на итерации ![]() появляется новая точка
появляется новая точка ![]() , доминирующая некоторые точки из архива
, доминирующая некоторые точки из архива ![]() , то все доминируемые точки, а также соответствующие точки из архива
, то все доминируемые точки, а также соответствующие точки из архива ![]() , удаляем. При удовлетворении некоторого критерия останова текущее содержимое архивов
, удаляем. При удовлетворении некоторого критерия останова текущее содержимое архивов ![]() ,
, ![]() полагаем искомой аппроксимацией фронта Парето
полагаем искомой аппроксимацией фронта Парето ![]() и множества Парето
и множества Парето ![]() соответственно.
соответственно.
В популяционных методах Парето-аппроксимации новые точки для архивов ![]() ,
, ![]() «поставляет» популяция агентов
«поставляет» популяция агентов ![]() , текущие координаты которых в пространстве поиска
, текущие координаты которых в пространстве поиска ![]() равны
равны ![]() , а в пространстве
, а в пространстве ![]() ‑
‑ ![]() .
.
В популяционных оптимизационных алгоритмах миграция агентов в пространстве поиска подчинена задаче минимизации (для определенности) значений фитнесс-функции. Основной проблемой построения популяционных методов Парето-аппроксимации является построение фитнесс-функции ![]() , обеспечивающей перемещение агентов популяции
, обеспечивающей перемещение агентов популяции ![]() ,
, ![]() в направлении множества Парето
в направлении множества Парето ![]() , а соответствующих точек
, а соответствующих точек ![]() ‑ в направлении фронта Парето
‑ в направлении фронта Парето ![]() .
.
В силу, как правило, меньшей размерности критериального пространства ![]() по сравнению с размерностью пространства поиска
по сравнению с размерностью пространства поиска ![]() , ответ на вопрос о направлении и шаге перемещения агентов обычно отыскивают в терминах критериального пространства, а не пространства параметров. Важно также, что относительно множества Парето, по сути, нет никой априорной информации, кроме того, что это множество точек, не связанных между собой отношением предпочтения
, ответ на вопрос о направлении и шаге перемещения агентов обычно отыскивают в терминах критериального пространства, а не пространства параметров. Важно также, что относительно множества Парето, по сути, нет никой априорной информации, кроме того, что это множество точек, не связанных между собой отношением предпочтения ![]() . В то же время по отношению к фронту Парето априорной информации значительно больше. Например, с учетом того, что частные критерии оптимальности нормированы и поэтому
. В то же время по отношению к фронту Парето априорной информации значительно больше. Например, с учетом того, что частные критерии оптимальности нормированы и поэтому ![]() , имеет место
, имеет место
Утверждение 1. Любой луч, проведенный из начала системы координат ![]() в неотрицательном направлении осей
в неотрицательном направлении осей ![]()
![]() ,…,
,…,![]() пересекает фронт Парето не более чем в одной точке.
пересекает фронт Парето не более чем в одной точке.
Доказательство проведем от противного. Допустим, что утверждение неверно, и указанный луч пересекает фронт Парето в точках ![]() ,
, ![]() . В этом случае, по крайней мере, для одного
. В этом случае, по крайней мере, для одного ![]() должно быть справедливо неравенство
должно быть справедливо неравенство ![]() или неравенство
или неравенство ![]() , что противоречит условию принадлежности точек
, что противоречит условию принадлежности точек ![]() ,
, ![]() фронту Парето●
фронту Парето●
Выделяют четыре класса задач Парето-оптимизации, соответствующих следующим четырем типам фронта Парето: выпуклые задачи; вогнутые задачи; выпукло-вогнутые задачи; разрывные задачи (рисунок 2).
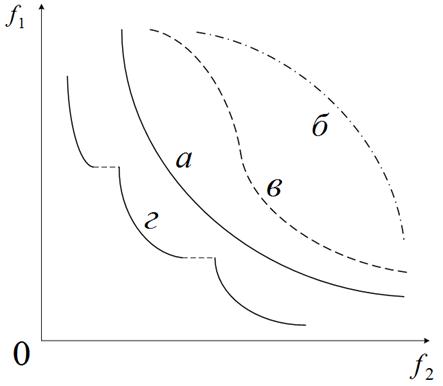
Рисунок 2 – Типы фронтов Парето (![]() ): а) выпуклый; б) вогнутый; в) выпукло-вогнутый фронт; г) разрывный
): а) выпуклый; б) вогнутый; в) выпукло-вогнутый фронт; г) разрывный
Одной из проблем популяционных методов Парето-аппроксимации является формирование начальных состояний архивов ![]() ,
, ![]() . С этой целью может быть использован сеточный метод, суть которого состоит в следующем. Покрываем область
. С этой целью может быть использован сеточный метод, суть которого состоит в следующем. Покрываем область ![]() некоторой сеткой с узлами
некоторой сеткой с узлами ![]() ,
, ![]() . В каждом из этих узлов вычисляем значение вектор-функции
. В каждом из этих узлов вычисляем значение вектор-функции ![]() , среди векторов
, среди векторов ![]() выбираем недоминируемые векторы
выбираем недоминируемые векторы ![]() и находим соответствующее им множество точек
и находим соответствующее им множество точек ![]() , где
, где ![]() ,
, ![]() . Множества
. Множества ![]() ,
, ![]() представляют собой искомую начальную дискретную аппроксимацию множества Парето и фронта Парето МКО-задачи (1) соответственно.
представляют собой искомую начальную дискретную аппроксимацию множества Парето и фронта Парето МКО-задачи (1) соответственно.
Известным вариантом сеточного метода является метод исследования пространства параметров [15], особенностью которого является использование специальных сеток, построенных на основе так называемых ![]() последовательностей, обеспечивающих большую репрезентативность Парето-аппроксимации.
последовательностей, обеспечивающих большую репрезентативность Парето-аппроксимации.
2. «Наивные» методы
Данный класс методов выделяет Люк (S. Luke) в своей известной книге [14]. Простейшим методом данного класса является метод на основе лексикографической турнирной селекции (lexicographictournamentselection).
Метод исходит из того, что частные критерии ![]() упорядочены по важности, так что самым важным является критерий
упорядочены по важности, так что самым важным является критерий ![]() , следующим по важности – критерий
, следующим по важности – критерий ![]() и так далее. Рассмотрим правило сравнения приспособленностей агентов, используемое данным методом. Пусть
и так далее. Рассмотрим правило сравнения приспособленностей агентов, используемое данным методом. Пусть ![]() - два сравниваемых агента в текущих состояниях
- два сравниваемых агента в текущих состояниях ![]() . Лучшего из этих агентов определяем путем последовательного сравнения пар величин
. Лучшего из этих агентов определяем путем последовательного сравнения пар величин ![]() ,
, ![]() до тех пор, пока не будет установлено, что, например,
до тех пор, пока не будет установлено, что, например, ![]() . В таком случае полагаем, что агент
. В таком случае полагаем, что агент ![]() имеет лучшую приспособленность по сравнению с агентом
имеет лучшую приспособленность по сравнению с агентом ![]() .
.
Лучшего агента ![]() популяции в ее текущем состоянии
популяции в ее текущем состоянии ![]() определяем в результате следующей последовательности шагов.
определяем в результате следующей последовательности шагов.
1) Выбираем случайного агента популяции ![]() и полагаем его лучшим агентом, т.е. полагаем
и полагаем его лучшим агентом, т.е. полагаем ![]() . Выполняем присваивание
. Выполняем присваивание ![]() .
.
2) Выбираем другого случайного агента ![]() .
.
3) По указанному выше правилу определяем лучшего из агентов ![]() и объявляем его новым агентом
и объявляем его новым агентом ![]() .
.
4) Если ![]() (размер турнира
(размер турнира ![]() не исчерпан), то полагаем
не исчерпан), то полагаем ![]() и возвращаемся к шагу 2.
и возвращаемся к шагу 2.
Известен ряд модификаций рассмотренного метода. Так для выбора лучшего агента можно использовать случайный критерий из числа критериев ![]() . Можно использовать процедуру голосования, когда лучшим считается агент, которому соответствуют наименьшие значения наибольшего числа критериев. Наконец, можно использовать многоуровневую турнирную селекцию (в случае
. Можно использовать процедуру голосования, когда лучшим считается агент, которому соответствуют наименьшие значения наибольшего числа критериев. Наконец, можно использовать многоуровневую турнирную селекцию (в случае ![]() ), когда основной турнир проводим на основании одного критерия, однако агентов для этого турнира отбираем с использованием турнира по другому критерию, агентов для этого турнира отбираем с использованием турнира по третьему критерию и т.д.
), когда основной турнир проводим на основании одного критерия, однако агентов для этого турнира отбираем с использованием турнира по другому критерию, агентов для этого турнира отбираем с использованием турнира по третьему критерию и т.д.
3. Методы переключающихся целевых функций
В данных методах выбор лучших агентов популяции производится на основе сравнения соответствующих значений различных частных критериев оптимальности. Наиболее известным алгоритмом Парето-аппроксимации, основанном на методе переключающихся целевых функций, является алгоритм VEGA(VectorEvaluatedGeneticAlgorithm), предложенный Шафером (D. Shaffer) в 1985 г. [16].
Пусть ![]() текущие положения агентов популяции, где
текущие положения агентов популяции, где ![]() и эти величины кратны. Пригодность агентов в алгоритме VEGAопределяют по следующей схеме.
и эти величины кратны. Пригодность агентов в алгоритме VEGAопределяют по следующей схеме.
1) В соответствии с принятым правилом селекции, основываясь на фитнесс-функции ![]() , выбираем
, выбираем ![]() лучших агентов, не исключая их из популяции.
лучших агентов, не исключая их из популяции.
2) Аналогично, основываясь на фитнесс-функции ![]() , выбираем следующие
, выбираем следующие ![]() лучших агентов.
лучших агентов.
….
![]() Основываясь на фитнесс-функции
Основываясь на фитнесс-функции ![]() , выбираем
, выбираем ![]() последних лучших агентов.
последних лучших агентов.
В качестве правила селекции алгоритм VEGA использует правило рулетки, когда вероятность выбора агента ![]() пропорциональна его относительной приспособленности (если речь идет о максимизации целевых функций):
пропорциональна его относительной приспособленности (если речь идет о максимизации целевых функций):
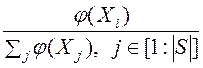 ,
, ![]() .
.
Рассмотренную схему отбора иллюстрирует рисунок 3, на котором представлены проекции точек ![]() на плоскость
на плоскость ![]() пространства критериев
пространства критериев ![]() . Показаны множества агентов
. Показаны множества агентов ![]() , отобранных на основе критериев оптимальности
, отобранных на основе критериев оптимальности ![]() ,
, ![]() соответственно (имеются в виду задача многокритериальной максимизации).
соответственно (имеются в виду задача многокритериальной максимизации).
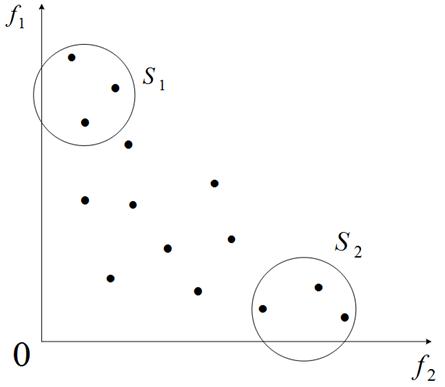
Рисунок 3 – К схеме алгоритма VEGA
4. Методы агрегации целевых функций
В данном случае целевые функции агрегируют (сворачивают) в один параметризованный скалярный критерий, который выступает в роли фитнесс-функции. Рассматриваем следующие методы данного класса: метод взвешенных критериев; метод идеальной точки; адаптивный метод взвешенных сумм.
4.1. Метод взвешенных критериев
Теоретической основой метода взвешенных критериев (SumofWeightedObjectives, SWO) является следующая известная теорема [1, 2].
Теорема 1. Если для некоторых весовых множителей ![]() ,
, ![]() имеет место равенство
имеет место равенство
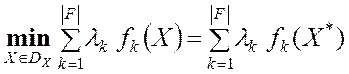 , (2)
, (2)
где ![]() , то вектор
, то вектор ![]() оптимален по Парето.
оптимален по Парето.
Доказательство. Пусть вектор ![]() не оптимален по Парето. Тогда существует такой вектор
не оптимален по Парето. Тогда существует такой вектор ![]() , что
, что
![]() ,
, ![]() ,
,
причем хотя бы одно из неравенств является строгим. Умножая каждое из последних неравенств на ![]() и складывая, получим
и складывая, получим
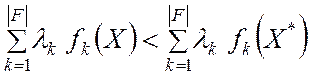 ,
,
что противоречит условию теоремы●
Теорема 1 показывает, что выбор определенной точки из множества Парето эквивалентен указанию весов для каждого из частных критериев оптимальности. Важно, что теорема задает лишь необходимое условие оптимальности по Парето вектора ![]() . Т.е. из того факта, что точка
. Т.е. из того факта, что точка ![]() принадлежит множеству Парето, не следует, что эта точка обязательно удовлетворяет условию (2) – случай невыпуклого множества
принадлежит множеству Парето, не следует, что эта точка обязательно удовлетворяет условию (2) – случай невыпуклого множества ![]() (рисунок 4).
(рисунок 4).

Рисунок 4 – Невыпуклый фронт Парето: ![]() ; дуга
; дуга ![]() - фронт Парето
- фронт Парето ![]()
В качестве фитнесс-функции в методе взвешенных критериев используем функцию
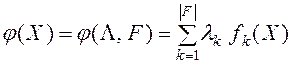 ,
,
где ![]() -вектор
-вектор ![]() . Основным недостатком метода является невозможность с его помощью локализовать точки фронта Парето, принадлежащие его невыпуклой части (дуга
. Основным недостатком метода является невозможность с его помощью локализовать точки фронта Парето, принадлежащие его невыпуклой части (дуга ![]() на рисунке 4).
на рисунке 4).
Метод широко используется для построения не популяционных алгоритмов Парето-аппроксимации, схема которых состоит из двух следующих основных шагов.
1) Множество ![]() допустимых значений вектора весовых множителей
допустимых значений вектора весовых множителей ![]() покрываем некоторой сеткой с узлами
покрываем некоторой сеткой с узлами ![]() ,
, ![]()
2) При каждом ![]() решаем задачу глобальной условной оптимизации (2) – получают точку
решаем задачу глобальной условной оптимизации (2) – получают точку ![]() .
.
4.2. Метод идеальной точки
Идеальной называют точку в пространстве критериев ![]() , где
, где
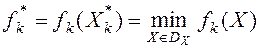 ,
, ![]() .
.
В качестве фитнесс-функции в этом случае используют функцию
![]() , (3)
, (3)
где ![]() ‑ некоторая метрика пространства
‑ некоторая метрика пространства ![]() , например, чебышевская метрика [17]
, например, чебышевская метрика [17]
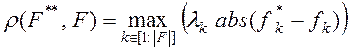 ,
, ![]() .
.
Здесь ![]() ‑ символ абсолютного значения числа.
‑ символ абсолютного значения числа.
Метод идеальной точки иллюстрирует рисунок 5, показывающий, что, в отличие от метода взвешенных критериев, данный метод позволяет отыскивать точки, лежащие на невыпуклой части фронта Парето. Заметим, что свертка на основе идеальной точки (3) близка к свертке Гермейера [17].
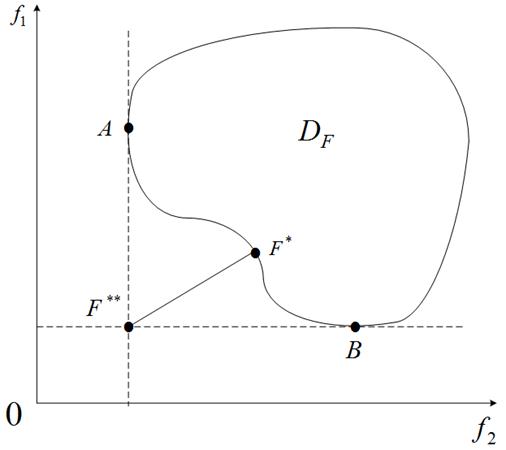
Рисунок 5 – К методу идеальной точки: ![]() ; дуга
; дуга ![]() - фронт Парето
- фронт Парето
Метод может быть использован для построения не популяционных алгоритмов Парето-аппроксимации. Задачу Парето-аппроксимации в этом случае сводят к многократному решению задачи глобальной оптимизации
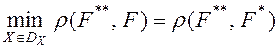
при различных допустимых значениях компонентов вектора весов ![]() по схеме, близкой к схеме, приведенной в предыдущем пункте.
по схеме, близкой к схеме, приведенной в предыдущем пункте.
4.3. Адаптивный метод взвешенных сумм
Адаптивный метод взвешенных сумм (AdaptiveWeightedSumMethod, AWSM) предложили Рю, Ким и Ван (J-H. Ryu, S. Kim, H. Wan) в 2009 г. [18]. Целью разработки метода было преодоление указанного выше ограничения метода взвешенных критериев, заключающегося в невозможности отыскания точек, принадлежащих невыпуклым частям фронта Парето. Метод не является популяционным. Мы включаем его в обзор вследствие новизны и высокого потенциала развития.
Метод разработан для двухкритериальной задачи (![]() ) и включает в себя три следующие основные процедуры:
) и включает в себя три следующие основные процедуры:
• определение центральной точки;
• формирование метамоделей частных критериев;
• решение полученных оптимизационных задач.
Рассмотрим суть указанных процедур.
Определение центральной точки. На этапе инициализации центральная точка ![]() выбирается случайным образом в области
выбирается случайным образом в области ![]() . На этом же этапе должны быть определены следующие свободные параметры метода:
. На этом же этапе должны быть определены следующие свободные параметры метода: ![]() ‑ начальный радиус области доверия (trustregionradius);
‑ начальный радиус области доверия (trustregionradius); ![]() ‑ коэффициент сужения области доверия;
‑ коэффициент сужения области доверия; ![]() ‑ минимальная величина радиуса области доверия.
‑ минимальная величина радиуса области доверия.
На итерации ![]() центральная точка
центральная точка ![]() отыскивается среди точек текущей Парето-аппроксимации
отыскивается среди точек текущей Парето-аппроксимации ![]() , построенной на предыдущей итерации
, построенной на предыдущей итерации ![]() .
.
Отсортируем элементы архивных множеств ![]() по возрастанию первого частного критерия оптимальности
по возрастанию первого частного критерия оптимальности ![]() и представим в виде линейных списков с прежними наименованиями. Определим расстояние
и представим в виде линейных списков с прежними наименованиями. Определим расстояние ![]() архивной точки
архивной точки ![]() до ближайших к ней в списке
до ближайших к ней в списке ![]() точек формулой
точек формулой
где ![]() ‑ символ евклидовой нормы.
‑ символ евклидовой нормы.
Метод использует следующее правило определения центральной точки ![]() .
.
1) Если ![]() , то полагаем
, то полагаем ![]() , где
, где
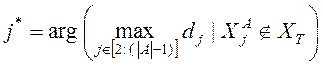 .
.
Здесь ![]()
![]() - множество точек, использованных в качестве центральных на всех предыдущих итерациях
- множество точек, использованных в качестве центральных на всех предыдущих итерациях ![]() . Иными словами, за центральную точку принимаем точку, во-первых, наиболее удаленную от других точек множества
. Иными словами, за центральную точку принимаем точку, во-первых, наиболее удаленную от других точек множества ![]() в смысле расстояния (4), и, во-вторых, не использованную на предшествующих итерациях.
в смысле расстояния (4), и, во-вторых, не использованную на предшествующих итерациях.
2) Если ![]() , то с равной вероятностью полагаем
, то с равной вероятностью полагаем ![]() или
или ![]() .
.
3) Если ![]() , то принимаем
, то принимаем ![]() .
.
Формирование метамоделей. Метамодели представляют собой квадратичные аппроксимации ![]() ,
, ![]() функций
функций ![]() ,
, ![]() в окрестности точки
в окрестности точки ![]() :
:
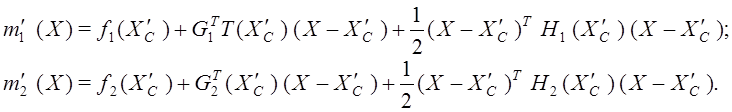
Здесь ![]() - символ транспонирования;
- символ транспонирования; ![]() ‑ градиенты функций
‑ градиенты функций ![]() ,
, ![]() в точке
в точке ![]() соответственно;
соответственно; ![]() ‑ матрицы Гессе этих функций.
‑ матрицы Гессе этих функций.
Если ![]() , то дополнительно строим метамодели
, то дополнительно строим метамодели
![]() ,
,
![]() ,
,
а если ![]() или
или ![]() ‑ метамодель
‑ метамодель
![]() .
.
В первом случае (![]() ) весовые множители
) весовые множители ![]() ,
, ![]() определяем по правилу
определяем по правилу
![]() ,
,
![]() ;
;
во втором случае (![]() ) – по правилу
) – по правилу
![]() ;
;
в третьем случае (когда ![]() ) – по правилу
) – по правилу ![]() . Константы
. Константы ![]() ,
, ![]() выбираем таким образом, чтобы обеспечить выполнение условий нормировки
выбираем таким образом, чтобы обеспечить выполнение условий нормировки ![]() .
.
Отметим, что при построении метамоделей ![]() ,
, ![]() речь может идти не о градиентах и матрице Гессе функций
речь может идти не о градиентах и матрице Гессе функций ![]() ,
, ![]() , а об их оценках, полученных, например, численными методами (путем соответствующих конечно-разностных аппроксимаций указанных функций).
, а об их оценках, полученных, например, численными методами (путем соответствующих конечно-разностных аппроксимаций указанных функций).
Решение оптимизационных задач. Данная процедура предполагает решение задач оптимизации

 (5)
(5)
где текущая область доверия ![]() определяет формула
определяет формула
![]() .
.
Если ![]() , то решения
, то решения ![]() задач (5) позволяют отыскать приближенно оптимальные по Парето точки
задач (5) позволяют отыскать приближенно оптимальные по Парето точки ![]() , принадлежащие области доверия
, принадлежащие области доверия ![]() , путем решения оптимизационных задач
, путем решения оптимизационных задач
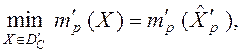
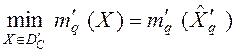 . (6)
. (6)
Данный этап метода AWSMиллюстрирует рисунок 6, на котором принято что ![]() ,
, ![]() ,
, ![]() . Отметим, что задачи (5), (6) представляют собой задачи оптимизации квадратичных функций, для решения которых известны высокоэффективные методы, алгоритмы и соответствующее программное обеспечение.
. Отметим, что задачи (5), (6) представляют собой задачи оптимизации квадратичных функций, для решения которых известны высокоэффективные методы, алгоритмы и соответствующее программное обеспечение.
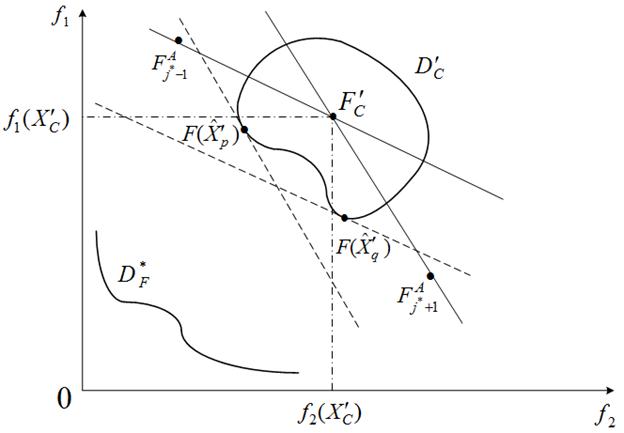
Рисунок 6 – К схеме адаптивного метода взвешенных сумм: результаты решения задач (6)
В процессе итераций текущий радиус области доверия уменьшают по правилу ![]() до достижения минимально допустимой его величины
до достижения минимально допустимой его величины ![]() . Новое состояние архивного множества
. Новое состояние архивного множества ![]() получаем путем добавления в текущее множество
получаем путем добавления в текущее множество ![]() точек
точек ![]() ,
, ![]() ,
, ![]() ,
, ![]() и исключения из полученного набора доминируемых решений. Множество
и исключения из полученного набора доминируемых решений. Множество ![]() образуют точки, соответствующие построенному множеству
образуют точки, соответствующие построенному множеству ![]() .
.
5. Методы на основе ранжирования агентов популяции
Основным понятием методов данного класса является понятие ранга агента популяции. Известно несколько правил вычисления рангов. Ниже рассмотрены основные из этих правил, используемые в методе недоминируемой сортировки, методе Парето-силы, а также в некоторых других методах.
5.1. Недоминируемая сортировка
Метод недоминируемой сортировки (Non-DominatedSorting, NDS) впервые был опубликован в работе Шриниваса (N. Srinivas) и Деба (K. Deb) в 1994 г. [19]. Метод лежит в основе широко известного генетического алгоритма Парето-аппроксимации NGSA (Non-DominatedSortingGeneticAlgorithm) [21].
Положим, что все частные критерии оптимальности являются одинаково важными. Ранг агента ![]() ,
, ![]() в его текущем положении
в его текущем положении ![]() обозначаем
обозначаем ![]() . В методе NDSиспользуется простейшее из правил вычисления рангов, имеющее следующий вид (рисунок 7).
. В методе NDSиспользуется простейшее из правил вычисления рангов, имеющее следующий вид (рисунок 7).
1) Выбираем среди всех агентов популяции недоминируемых, присваиваем им ранг, равный единице, и исключаем из дальнейшего рассмотрения.
2) Среди оставшихся агентов выбираем недоминируемых, присваиваем им ранг, равный двум, и исключаем из дальнейшего рассмотрения. И так далее до исчерпания популяции.
Ранг индивида легко использовать для вычисления его приспособленности, например, по формуле вида
 ,
, ![]() .
.
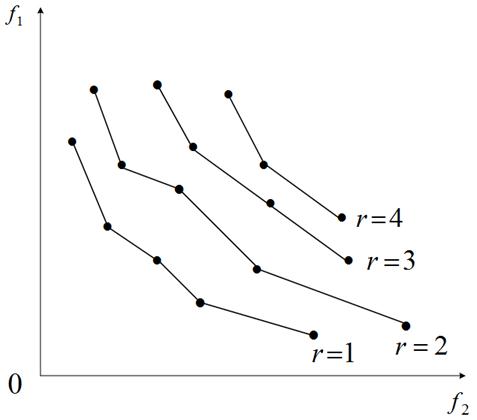
Рисунок 7 – К определению понятия ранга агента: ![]()
Предтечей метода недоминируемой сортировки можно, вероятно, считать метод MOGA− (Multi-ObjectiveGeneticAlgorithm), предложенный Фонсека (C. M. Fonseca) и Флемингом (P. J. Fleming) в 1993 г. [10]. В методе предполагается, что ранг агента равен числу агентов в популяции, которые его доминирует. Заслуживает также упоминания Парето генетический алгоритм с нишеванием (Niched-ParetoGeneticAlgorithm, NPGA), предложенный Хорном (J. Horn) cсоавторами в 1994 г. [20].
Как отмечалось выше, важнейшим требованием к методам и алгоритмам Парето-аппроксимации является требование обеспечения равномерности покрытия множества и фронта Парето. Для оценки равномерности покрытия может быть использована величина, называемая разреженностью (scarcity), имеющая смысл минимального расстояния между решениями, принадлежащими Парето-аппроксимации. Указанное расстояние может быть измерено с помощью различных метрик, например, с помощью известного манхеттеновского расстояния (Manhattandistance). Развитием метода недоминируемой сортировки является метод, в котором при формировании архивов ![]() отвергают агентов, расстояние которых до других агентов в архиве не превышает заданной величины. Такой модифицированный метод положен в основу генетического алгоритма Парето-аппроксимации NGSA-II (Non-DominatedSortingGeneticAlgorithmII) [21].
отвергают агентов, расстояние которых до других агентов в архиве не превышает заданной величины. Такой модифицированный метод положен в основу генетического алгоритма Парето-аппроксимации NGSA-II (Non-DominatedSortingGeneticAlgorithmII) [21].
5.2. Метод Парето-силы
Иное правило ранжирования агентов популяции используется в методе Парето силы (Paretostrength). Метод исходит из того, что сила агента ![]() ,
,![]() равна числу особей, которых доминирует по Парето данный агент. Определенную указанным способом силу агентов можно использовать для вычисления их приспособленности. Однако такое определение пригодности обладает рядом недостатков [14]. Поэтому в вычислительной практике используют альтернативное понятие слабости (weakness) агента, равной числу особей, его доминирующих. Точнее говоря, используют вариант слабости агента, называемый в работе [14] его хилостью (wimpiness)
равна числу особей, которых доминирует по Парето данный агент. Определенную указанным способом силу агентов можно использовать для вычисления их приспособленности. Однако такое определение пригодности обладает рядом недостатков [14]. Поэтому в вычислительной практике используют альтернативное понятие слабости (weakness) агента, равной числу особей, его доминирующих. Точнее говоря, используют вариант слабости агента, называемый в работе [14] его хилостью (wimpiness) ![]() и равный суммарной силе всех особей, доминирующих данного агента. Фитнесс-функция при этом имеет вид
и равный суммарной силе всех особей, доминирующих данного агента. Фитнесс-функция при этом имеет вид
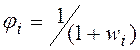 ,
, ![]() .
.
Метод Парето силы использует известный популяционный алгоритм Парето-аппроксимации SPEA (StrengthParetoEvolutionaryAlgorithm) [21]. Развитием алгоритма SPEAявляется алгоритм SPEA-2, который подобно алгоритму NGSA-IIиспользует оценки равномерности Парето-аппроксимации [23].
Упрощенным вариантом алгоритма SPEA-2 можно считать алгоритм PAES(ParetoAchievedEvolutionStrategy), предложенный Ноулзом (J. Knowles) и Корн (D. Corne) в 1999 г. [24]. Рангом ![]() агента
агента ![]() в алгоритме PAESназывается число архивных решений, доминируемых решением
в алгоритме PAESназывается число архивных решений, доминируемых решением ![]() . Схема алгоритмаPAES для агента
. Схема алгоритмаPAES для агента ![]() имеет следующий вид.
имеет следующий вид.
1) По законам используемого популяционного алгоритма (в оригинале – генетического алгоритма) перемещаем агента ![]() из его текущего положения
из его текущего положения ![]() в новое положение
в новое положение ![]() .
.
2) Если одно из решений ![]() и
и ![]() доминирует другое решение, то лучшее из них объявляем кандидатом. В противном случае кандидатом объявляем то из решений
доминирует другое решение, то лучшее из них объявляем кандидатом. В противном случае кандидатом объявляем то из решений ![]() ,
, ![]() , ранг которого выше.
, ранг которого выше.
3) Если решение-кандидат доминируется некоторым из архивных решений, то кандидата отвергаем. В противном случае кандидата записываем в архив, но только в том случае, если он находится в той части области поиска, в которой на текущий момент обнаружено мало решений. При записи кандидата в архив все доминируемые им решения из архива удаляем.
4) Если условие окончания итераций не выполнено, возвращаемся к шагу 1.
5.3. Другие методы на основе ранжирования
Метод средневзвешенного ранжирования (WeightedAverageRanking, WAR) предложили Бентли (P. J. Bentley) и Вэйкфилд (J. P. Wakefield) в 1996 г. [25]. Пусть ![]() ‑ относительная важность частного критерия
‑ относительная важность частного критерия ![]() . Метод WAR предполагает вычисление текущего ранга агента
. Метод WAR предполагает вычисление текущего ранга агента ![]() по следующей схеме.
по следующей схеме.
1) Для каждого из критериев ![]() формируем список
формируем список ![]() , содержащий величины
, содержащий величины ![]() , упорядоченные по их возрастанию.
, упорядоченные по их возрастанию. ![]()
2) Ранг агента ![]() полагаем равным величине
полагаем равным величине
![]() ,
, ![]() , (7)
, (7)
где ![]() - порядковый номер агента
- порядковый номер агента ![]() в списке
в списке ![]() .
.
Метод суммы взвешенных оценок (SumofWeightedRatios, SWR) можно считать развитием метода WAR [25]. При вычислении ранга агентов метод использует свертку вида (7), в которой вместо относительной важности частных критериев ![]() используются их особым образом нормализованные значения. Нормализация основана на использовании наихудших и наилучших текущих значений критериев
используются их особым образом нормализованные значения. Нормализация основана на использовании наихудших и наилучших текущих значений критериев
 ,
, 
и определяется формулой
Метод суммы взвешенных глобальных оценок (SumofWeightedGlobalRatios, SWGR) [25] близок к предыдущему методу с тем отличием, что наихудшие и наилучшие значения критериев определяют на основе всей предыстории поиска, т.е. на основе всех итераций ![]() :
:
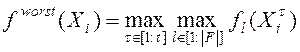 ;
; 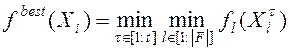 ;
; ![]() .
.
Метод максимального взвешенного ранжирования(WeightedMaximumRanking, WMR) [25] основан на идее рассмотренного выше метода VEGA. Положим, что все критерии нормализованы и заданы их относительные важности ![]() ,
, ![]() . Схему метода определяет следующая последовательно шагов.
. Схему метода определяет следующая последовательно шагов.
1) Аналогично методу WAR формируем списки ![]() ,
, ![]() и определяем величины
и определяем величины ![]() ,
, ![]() .
.
2) Вычисляем ранги каждого из ![]() агентов по всем
агентов по всем ![]() критериям оптимальности
критериям оптимальности
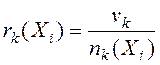 ,
, ![]() ,
, ![]() .
.
3) В качестве итогового ранга агента ![]() в его текущем положении
в его текущем положении ![]() принимаем величину
принимаем величину
![]() ,
, ![]() .
.
6. Прочие методы
В данном разделе рассматриваем сигма-метод, методы композитных точек, гиперкубов, динамических соседей, а также метод хищник-жертва.
6.1. Сигма-метод
Сигма-метод (sigmamethod) предложили Мостагхим (S. Mostaghim) и Тич (J. Teich) в 2003 г. [26].
Для двухкритериальной задачи (![]() ) сигма-параметром точки
) сигма-параметром точки ![]() или соответствующей ей точки
или соответствующей ей точки ![]() , называется величина
, называется величина
Легко видеть, что точки ![]() , имеющие одно и то же значение сигма-параметра, лежат на одной прямой, проходящей через начало системы координат
, имеющие одно и то же значение сигма-параметра, лежат на одной прямой, проходящей через начало системы координат ![]() . Определение сигма-параметра иллюстрирует рисунок 8, на котором одинаковые значения сигма-параметра имеют пары точек
. Определение сигма-параметра иллюстрирует рисунок 8, на котором одинаковые значения сигма-параметра имеют пары точек ![]() .
.
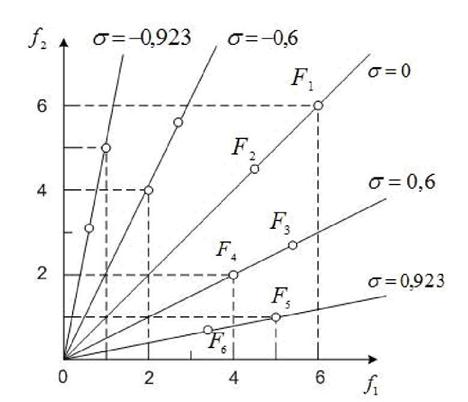
Рисунок 8 - К определению сигма-параметра: ![]()
В случае, когда размерность критериального пространства больше двух (![]() ) сигма-метод использует
) сигма-метод использует ![]() -мерный вектор сигма-параметров
-мерный вектор сигма-параметров ![]() . Для агента
. Для агента ![]() этот вектор определяет выражение
этот вектор определяет выражение
В сигма-методе для точки ![]() ,
, ![]() лучшая архивная точка
лучшая архивная точка ![]() ,
, ![]() определяется по следующей схеме.
определяется по следующей схеме.
1) Вычисляем значение сигма-параметра точки ![]() ‑ величину
‑ величину ![]() .
.
2) Находим в архиве ![]() точку
точку ![]() , у которой значение сигма-параметра наиболее близко к величине
, у которой значение сигма-параметра наиболее близко к величине ![]() :
:
Здесь ![]() ‑ символ евклидовой нормы.
‑ символ евклидовой нормы.
3) В качестве лучшей для точки ![]() принимаем точку
принимаем точку ![]() такую, что
такую, что ![]() .
.
В данном случае в качестве метрики близости точек ![]() ,
, ![]() используется евклидова норма в сигма-пространстве
используется евклидова норма в сигма-пространстве ![]() .
.
Утверждение 2. Предположим, что для всех архивных частиц ![]() вектор сигма-параметров
вектор сигма-параметров ![]() уже вычислен. Тогда отыскание для точки
уже вычислен. Тогда отыскание для точки ![]() лучшей архивной точки
лучшей архивной точки ![]() сигма-методом требует
сигма-методом требует ![]() арифметических операций.
арифметических операций.
Справедливость утверждения вытекает из того факта, что для отыскания точки, которая является лучшей для точки ![]() , требуется
, требуется ![]() раз вычислить значение нормы вида (8) и для каждого такого вычисления необходимо
раз вычислить значение нормы вида (8) и для каждого такого вычисления необходимо ![]() арифметических операций
арифметических операций![]()
Для двухкритериальной задачи изложенную схему сигма-метода иллюстрирует рисунок 9. Стрелками на рисунке для каждой из точек ![]() показаны «притягивающие» точки
показаны «притягивающие» точки ![]() .
.
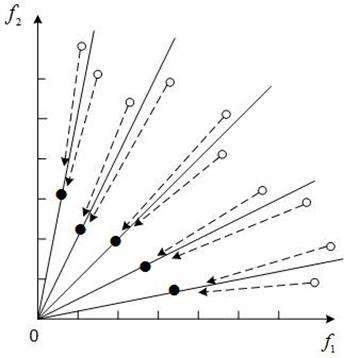
Рисунок 9 - Схема сигма-метода для двухкритериальной задачи:
![]() ‑ архивные точки
‑ архивные точки![]() ;
; ![]() ‑ точки
‑ точки ![]()
6.2. Метод композитных точек
Метод композитных точек предложили Филдсенд (J.E. Fieldsend) и Синх (S. Singh) в 2002 г. [27]. Метод использует архив ![]() недоминируемых точек в виде, так называемого дерева доминирования (dominatedtree), представляющего собой список композитных точек (compositepoints)
недоминируемых точек в виде, так называемого дерева доминирования (dominatedtree), представляющего собой список композитных точек (compositepoints) ![]() ,
, ![]() Для двухкритериальной задачи пример дерева доминирования приведен на рисунке 10.
Для двухкритериальной задачи пример дерева доминирования приведен на рисунке 10.
Координаты первой композитной точки ![]() определяем по следующей схеме.
определяем по следующей схеме.
1) В качестве первой координаты ![]() этой композитной точки принимаем первую координату той архивной точки
этой композитной точки принимаем первую координату той архивной точки ![]() , у которой значение этой координаты наибольшее, т.е. полагаем
, у которой значение этой координаты наибольшее, т.е. полагаем
Исключаем точку ![]() из дальнейшего рассмотрения.
из дальнейшего рассмотрения.
2) Вторую координату ![]() точки
точки ![]() полагаем равной второй координате той из оставшихся архивных точек
полагаем равной второй координате той из оставшихся архивных точек ![]() , у которой эта координата имеет наибольшее значение, т.е. принимаем, что
, у которой эта координата имеет наибольшее значение, т.е. принимаем, что
Точку ![]() исключаем из дальнейшего рассмотрения.
исключаем из дальнейшего рассмотрения.
3) Если ![]() , то поступаем аналогичным образом для всех остальных координат, так что
, то поступаем аналогичным образом для всех остальных координат, так что
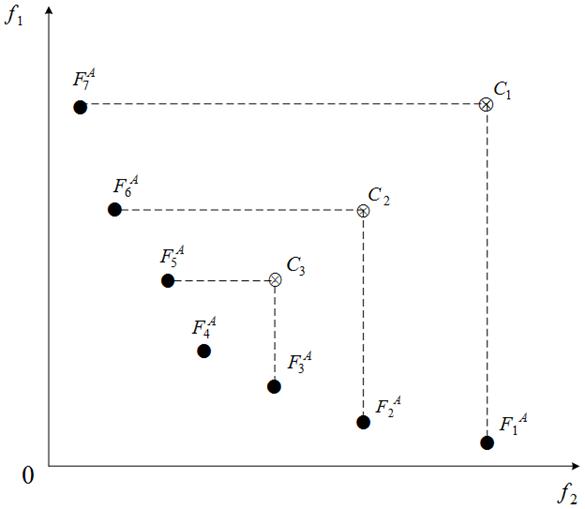
Рис. 10. Дерево доминирования для двухкритериальной задачи:![]() – архивные точки
– архивные точки ![]() ;
; ![]() – композитные точки
– композитные точки ![]()
4) По аналогичной схеме вычисляем координаты второй композитной точки ![]() и так далее до исчерпания всех точек архива
и так далее до исчерпания всех точек архива ![]() .
.
Рассмотрим схему алгоритма быстрого построения дерева доминирования. Положим, что сформированы списки ![]() из
из ![]() элементов каждый такие, что в списке
элементов каждый такие, что в списке ![]() содержатся точки архива
содержатся точки архива ![]() , отсортированные в порядке убывания по критерию оптимальности
, отсортированные в порядке убывания по критерию оптимальности ![]() ;
; ![]() . При использовании известного алгоритма быстрой сортировки построение таких списков требует, в худшем случае,
. При использовании известного алгоритма быстрой сортировки построение таких списков требует, в худшем случае, ![]() операций сравнения. Элементы списка
операций сравнения. Элементы списка ![]() обозначим
обозначим ![]() ,
, ![]() .
.
1) В качестве координаты ![]() точки
точки ![]() принимаем
принимаем ![]() -ю координату элемента
-ю координату элемента ![]() и исключаем этот элемент из всех списков.
и исключаем этот элемент из всех списков.
2) В качестве координаты ![]() точки
точки ![]() принимаем
принимаем ![]() -ю координату элемента
-ю координату элемента ![]() и исключаем этот элемент из всех списков.
и исключаем этот элемент из всех списков.
3) И так далее до исчерпания всех списков ![]() ;
; ![]() .
.
Легко видеть, что архиву ![]() соответствует общее число композитных точек, равное
соответствует общее число композитных точек, равное 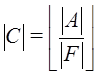 , где
, где ![]() - символ ближайшего целого меньшего.
- символ ближайшего целого меньшего.
Архивные точки ![]() , соответствующие композитной точке
, соответствующие композитной точке ![]() , назовем вершинами точки
, назовем вершинами точки ![]() .
.
После того как дерево доминирования построено, лучшую точку для точки ![]() определяем по следующему правилу.
определяем по следующему правилу.
1) В списке композитных точек находим точку ![]() такую, что имеет место хотя бы одно из неравенств
такую, что имеет место хотя бы одно из неравенств
2) Из числа вершин ![]() композитной точки
композитной точки ![]() находим точку
находим точку ![]() , которая строго доминирует точку
, которая строго доминирует точку ![]() , т.е. такую, что
, т.е. такую, что ![]() .
.
3) В качестве лучшей для точки ![]() принимаем точку
принимаем точку ![]() , соответствующую вершине
, соответствующую вершине ![]() .
.
4) Если среди вершин ![]() имеется более одной, которая строго доминирует точку
имеется более одной, которая строго доминирует точку ![]() , то из них случайным образом выбираем вершину
, то из них случайным образом выбираем вершину ![]() и в качестве лучшей для точки
и в качестве лучшей для точки ![]() принимаем соответствующую точку
принимаем соответствующую точку ![]() .
.
Рассмотренное правило определения лучшей точки иллюстрирует рисунок 11 , на котором стрелками на рисунке показаны соответствующие лучшие точки.

Рисунок 11 – К определению лучшей точки в методе композитных точек: ![]() – точки архива
– точки архива ![]() ;
; ![]() – композитные точки;
– композитные точки; ![]() - точки
- точки ![]()
Утверждение 3. Предположим, что дерево доминирования предварительно тем или иным образом построено. Тогда поиск в архиве ![]() точки, которая является лучшей для точки
точки, которая является лучшей для точки ![]() , требует
, требует ![]() сравнений.
сравнений.
Справедливость утверждения вытекает из того факта, что в изложенной схеме определения лучшей точки поиск композитной точки ![]() требует
требует ![]() , а выбор точки
, а выбор точки ![]() ‑ не более
‑ не более ![]() сравнений
сравнений![]()
6.3. Метод гиперкубов
В основе метода гиперкубов, предложенного Коэлло (C.A. Coello) и Лечунга (M.S. Lechunga) в 2002 г. [28], лежит процедура покрытия области достижимости ![]() некоторой совокупностью гиперкубов и процедура назначения каждому из этих гиперкубов коэффициента пригодности. Рассмотрим данные процедуры.
некоторой совокупностью гиперкубов и процедура назначения каждому из этих гиперкубов коэффициента пригодности. Рассмотрим данные процедуры.
Положим частные критерии оптимальности ![]() нормированными, так что
нормированными, так что ![]() ,
, ![]() .
.
Искомые гиперкубы строим путем разделения ![]() -мерного единичного гиперкуба
-мерного единичного гиперкуба ![]() на
на ![]() гиперкубов с длиной ребра, равной
гиперкубов с длиной ребра, равной ![]() (рисунок 12), где натуральное число
(рисунок 12), где натуральное число ![]() - свободный параметр метода.
- свободный параметр метода.
Пусть некоторый гиперкуб ![]() включает в себя
включает в себя ![]() архивных точек. Пригодность этого гиперкуба принимаем равной величине
архивных точек. Пригодность этого гиперкуба принимаем равной величине 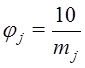 . Если выбранный гиперкуб вообще не содержит точек архива, то происходит расширение области поиска, т.е. вводится в рассмотрение гиперкуб, который включает в себя гиперкуб
. Если выбранный гиперкуб вообще не содержит точек архива, то происходит расширение области поиска, т.е. вводится в рассмотрение гиперкуб, который включает в себя гиперкуб ![]() . Таким образом, пригодность каждого из построенных гиперкубов полагаем обратно пропорциональной числу архивных точек, которые находятся в нем, и гиперкуб, содержащий меньшее число этих точек, оказывается более пригодным (рисунок 12). Такое определение пригодности направлено на обеспечение более равномерной Парето-аппроксимации.
. Таким образом, пригодность каждого из построенных гиперкубов полагаем обратно пропорциональной числу архивных точек, которые находятся в нем, и гиперкуб, содержащий меньшее число этих точек, оказывается более пригодным (рисунок 12). Такое определение пригодности направлено на обеспечение более равномерной Парето-аппроксимации.
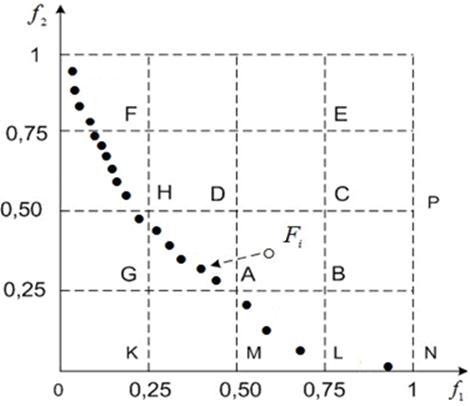
Рисунок 12 – Покрытие области ![]() гиперкубами для двухкритериальной задачи:
гиперкубами для двухкритериальной задачи: ![]() ;
; ![]() – архивные точки
– архивные точки ![]()
Если по рассмотренному правилу множество достижимости ![]() покрыто гиперкубами и для каждого из гиперкубов определены их пригодности, то отыскание в архиве
покрыто гиперкубами и для каждого из гиперкубов определены их пригодности, то отыскание в архиве ![]() точки, которая является лучшей для точки
точки, которая является лучшей для точки ![]() , производится по следующей схеме.
, производится по следующей схеме.
1) Если в гиперкубе ![]() , в котором находится точка
, в котором находится точка ![]() , имеются архивные точки, то случайным образом с равной вероятностью выбираем одну из этих точек
, имеются архивные точки, то случайным образом с равной вероятностью выбираем одну из этих точек ![]() .
.
2) В противном случае выполняем следующие действия:
- расширяем зону поиска ‑ рассматриваем все возможные гиперкубы ![]() с длиной ребра равной
с длиной ребра равной ![]() , которые включают в себя гиперкуб
, которые включают в себя гиперкуб ![]() ;
;
- определяем пригодность гиперкубов ![]() , как сумму пригодностей входящих в них гиперкубов
, как сумму пригодностей входящих в них гиперкубов ![]() ;
;
- из числа всех найденных гиперкубов ![]() по правилу рулетки выбираем один из гиперкубов
по правилу рулетки выбираем один из гиперкубов ![]() ;
;
- случайным образом с равной вероятностью выбираем одну из точек ![]() этого гиперкуба.
этого гиперкуба.
3) В качестве искомой лучшей точки принимаем соответствующую точку ![]() .
.
Приведенную схему выбора лучшей точки иллюстрирует рисунок 12. Точка ![]() на рисунке находится в гиперкубе
на рисунке находится в гиперкубе ![]() . В этом гиперкубе нет ни одной архивной точки. Поэтому в рассмотрение вводим гиперкубы
. В этом гиперкубе нет ни одной архивной точки. Поэтому в рассмотрение вводим гиперкубы ![]() . Пригодности этих гиперкубов равны 2; 2,3; 0,4 соответственно. По правилу рулетки выбираем, например, гиперкуб
. Пригодности этих гиперкубов равны 2; 2,3; 0,4 соответственно. По правилу рулетки выбираем, например, гиперкуб ![]() . В этом гиперкубе с равной вероятностью выбираем одну из архивных точек, например, точку, на которую на рисунке указывает стрелка.
. В этом гиперкубе с равной вероятностью выбираем одну из архивных точек, например, точку, на которую на рисунке указывает стрелка.
6.4. Метод динамических соседей
Метод динамических соседей предложили Хью (X. Hu) и Эберхарт (R. Eberhart) в 2002 г. [29]. Схему метода можно представить в следующем виде.
1) Фиксируем все критерии оптимальности, кроме критерия ![]() ‑ полагаем этот критерий динамическим.
‑ полагаем этот критерий динамическим.
2) Вычисляем в пространстве критериев ![]() расстояния (например, евклидовы) от точки
расстояния (например, евклидовы) от точки ![]() ,
, ![]() до всех архивных точек
до всех архивных точек ![]() .
.
3) Выбираем на этой основе ![]() ближайших архивных соседей точки
ближайших архивных соседей точки ![]() , где
, где ![]() - свободный параметр метода.
- свободный параметр метода.
4) Из числа выделенных точек выбираем лучшую по критерию ![]() .
.
5) На следующей итерации полагаем динамическим критерий ![]() , а все остальные критерии фиксируем. И так далее.
, а все остальные критерии фиксируем. И так далее.
Авторы метода отмечают, что остается открытым вопрос об оптимальной величине числа ![]() .
.
6.5. Метод хищник-жертва
Метод хищник-жертва (predator-prey) предложил Лауманс (M. Laumanns) с соавторами в 1998 г. [30]. Рассматриваем оригинальный метод Лауманса и его основные модификации последних лет. Полагаем, что областью допустимых значений вектора варьируемых параметров является гиперпараллелепипед
![]() .
.
Каждая из жертв представляет собой один вектор решений, а каждый хищник ‑ один критерий оптимальности. Популяция эволюционирует на тороидальной сетке (рисунок 13), в узлах которой случайным образом инициализируем жертв и хищников. Каждый хищник рассматривает все жертвы в своей окрестности и удаляет жертву с худшим значением соответствующего критерия оптимальности. Затем в той же окрестности выбираем и модифицируем случайную жертву. Измененное решение помещаем на место удаленной жертвы. Хищника случайным образом перемещаем в один из соседних с ним узлов сетки. Процесс итерационно повторяем до выполнения условий окончания.
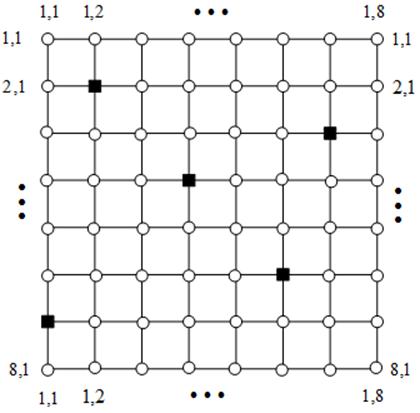
Рисунок 13 – Пример размещения хищников (квадратики) и жертв (кружки) на тороидальной сетке
Приведем схему метода в более формализованном виде.
1) В гиперпараллелепипеде ![]() случайным образом инициализируем популяцию жертв – решения
случайным образом инициализируем популяцию жертв – решения ![]() .
.
2) Ставим в соответствие жертвам вершины ненаправленного связного графа в виде тороидальной решетки.
3) Случайным образом помещаем хищников в вершины указанного графа.
4) Ставим в соответствие каждому из хищников один из критериев оптимальности ![]() таким образом, чтобы каждый из критериев был представлен, по меньшей мере, одним хищником.
таким образом, чтобы каждый из критериев был представлен, по меньшей мере, одним хищником.
5) Вычисляем значения соответствующего критерия для всех жертв в окрестности каждого из хищников и выбираем худшие жертвы.
6) Полагаем, что выбранные жертвы поглощены хищниками, и удаляем их из популяции.
7) Взамен каждого из удаленных агентов создаем новую жертву путем изменения случайно выбранной жертвы в окрестности удаленного агента.
8) Случайным образом перемещаем хищников из их текущих положений в соседние вершины графа.
9) Если условие окончания итераций не выполнено, возвращаемся к шагу 5.
Экспериментально показано, что с ростом числа поколений популяция жертв стремится к фронту Парето, т.е. представляет собой искомую Парето-аппроксимацию.
Недостатком рассмотренного канонического метода хищник-жертва является возможная потеря лучших (ближайших к множеству Парето решений).
Деб (K. Deb) в 2001 г. предложил улучшения метода [31], суть которых заключается в следующем:
- хищникам ставят в соответствие не частные критерии оптимальности, а векторы их весов;
- вместо удаленной жертвы новую жертву создают путем модификации не случайного, но лучшего агента в окрестности удаленной жертвы;
- хищника перемещают не случайным образом, а в направлении позиции лучшей жертвы в его окрестности.
Исследования авторов метода показывают, что он обеспечивает по сравнению с каноническим методом более высокую скорость сходимости, однако, как и канонический метод, может терять найденные лучшие решения.
В работе [32] рассмотрена модификация канонического метода, предложенная Ли (X. Li), в которой жертв и хищников помещают не во все узлы графа, представленного на рисунке 13. Жертвы и хищники выполняют случайные перемещения в направлении соседних пустых узлов графа, причем хищники движутся быстрее жертв. При каждом перемещении жертвы создается ее потомок. Вычислительные эксперименты показали недостаточно высокую скорость сходимости соответствующего алгоритма.
В той же работе [32] Дебом (K. Deb) и Рао (U. Rao) предложена глубокая модификация канонического метода, основу которой составляют следующие три механизма:
- механизм сохранения лучших решений;
- механизм рекомбинации решений;
- механизм получения равномерной Парето-аппроксимации.
Механизм сохранения лучших решений(элитизм) предполагает сравнения приспособленности худших жертв с приспособленностью созданных агентов (потомков). Меру приспособленности агентов строим на основе Парето доминирования. Если данный потомок слабо доминирует всех жертв популяции (лучше их, по крайней мере, по одному из частных критериев оптимальности), то заменяем этим потомком соответствующую худшую жертву. В противном случае потомка объявляем неподходящим, худшую жертву оставляем в популяции, а хищник для обеспечения разнообразия популяции случайным образом перемещаем в направлении худшей жертвы.
Механизм рекомбинации решений строим на основе операторов скрещивания и мутации агентов (так что, в целом, метод оказывается вариантом генетического алгоритма). В окрестности худшей жертвы создаем двух потомков путем скрещивания лучшего и второго лучшего решений. Затем случайным образом выбираем одного из этих потомков и выполняем его мутацию. Если полученный таким образом потомок оказывается хуже худшей жертвы, то по рассмотренной схеме создаем нового потомка и опять сравниваем его приспособленность с приспособленностью худшей жертвы. Процесс повторяем не более некоторого фиксированного числа раз.
Механизм обеспечения равномерности покрытия. Полагаем, что каждая жертва имеет область влияния (influencingregion) в виде гиперкуба в критериальном пространстве, в центре которого находится данная жертва. Потомка полагаем не подходящим, если он создан в области влияния любой из существующих жертв. Заметим, что аналогичный механизм используется в методе ![]() -доминирования [33]. Размеры области влияния назначаем, исходя из требуемой равномерности покрытия.
-доминирования [33]. Размеры области влияния назначаем, исходя из требуемой равномерности покрытия.
Для того чтобы предотвратить ситуацию, когда хищники полностью уничтожают популяцию, используем следующий прием. Число перемещений ![]() , которые выполняют хищники перед тем, как жертвы могут сделать свои перемещения, объявляем динамической переменной, определяемой формулой
, которые выполняют хищники перед тем, как жертвы могут сделать свои перемещения, объявляем динамической переменной, определяемой формулой
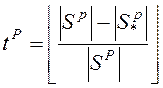 ,
,
где ![]() - символ ближайшего меньшего,
- символ ближайшего меньшего, ![]() ,
, ![]() - текущее и желаемое числа жертв,
- текущее и желаемое числа жертв, ![]() - текущее число хищников. В результате при уменьшении числа жертв уменьшается величина
- текущее число хищников. В результате при уменьшении числа жертв уменьшается величина ![]() , т.е. хищники начинают двигаться медленнее, шансы жертв на выживание повышаются, и популяция жертв расширяется. При этом хищники становятся более быстрыми, и их популяция начинает сокращаться. И так далее.
, т.е. хищники начинают двигаться медленнее, шансы жертв на выживание повышаются, и популяция жертв расширяется. При этом хищники становятся более быстрыми, и их популяция начинает сокращаться. И так далее.
Авторы рассматриваемой модификации метода выполнили широкое экспериментальное исследование его эффективности на ряде трудных задач известного тестового набора двух- и трехцелевых задач многокритериальной оптимизации [31]. Показано, что алгоритм обеспечивает высокие скорость сходимости и равномерность покрытия фронта-Парето.
Заключение
Многообразие методов построения Парето-аппроксимации указывает на актуальность данной задачи. Представляются перспективными следующие направления развития этих методов.
Вычислительная сложность частных критериев оптимальности, вообще говоря, различна в различных частях области варьируемых параметров ![]() . Рассмотренные и иные известные методы Парето-аппроксимации не учитывают этого обстоятельства. Поэтому актуальной, на наш взгляд, является разработка адаптивных и самоадаптивных методов Парето-аппроксимации, учитывающих данный факт.
. Рассмотренные и иные известные методы Парето-аппроксимации не учитывают этого обстоятельства. Поэтому актуальной, на наш взгляд, является разработка адаптивных и самоадаптивных методов Парето-аппроксимации, учитывающих данный факт.
Практически значимые задачи многокритериальной оптимизации имеют высокую вычислительную сложность и требуют для своего решения использования параллельных вычислительных систем. Поэтому необходима разработка параллельных методов Парето-аппроксимации, ориентированных на различные классы таких систем (кластерные системы, графические процессорные устройства и т.д.) [34].
Важным с практической точки зрения является класс задач Парето-аппроксимации, в которых требуется построить аппроксимацию не всего фронта Парето, но лишь той части его, которая ближе всего к заданной пользователем «предпочтительной» точке пространства критериев. Поэтому представляется актуальной задача разработки методов решения задач данного класса. Известна модификация метода хищник-жертва, предназначенная для решения таких задач [32]. Можно также считать, что метод идеальной точки является частным случаем этих методов.
Задачу Парето-аппроксимации можно считать одной из широкого класса задач приближенного построения границ множеств различной природы. Поэтому значительный интерес представляет адаптация рассмотренных методов и разработка новых методов, предназначенных для решения задач указанного класса. Пример такого подхода демонстрирует работа [35], в которой один из методов Парето-аппроксимации использован для приближенного построения границы области достижимости многосекционного манипулятора параллельной кинематики типа хобот.
Отметим, наконец, перспективность гибридизации рассмотренных и иных методов Парето-аппроксимации.
Авторы благодарят Бушневского А.В. и Савелова А.С. за помощь в подготовке некоторых материалов для данной работы.
Литература
1. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач.- М.: Физматлит, 2007.- 256 с.
2. Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход.- М.: Физматлит, 2005.- 176 с.
3. Ларичев О.И. Теория и методы принятия решений: Учебник для ВУЗов.- М.: Университетская книга, Логос, 2006.- 392 с.
4. Курейчик В.М. Генетические алгоритмы и их применение.- Таганрог: Изд-во Таганрогского РТУ, 2002. -244 с.
5. Ashlock D. Evolutionary Computation for Modeling and Optimization.- Springer, 2006.- 571 pp.
6. Guliashki V., Toshev H., Korsemov Ch. Survey of Evolutionary Algorithms Used in Multiobjective Optimization // Problems of Engineering Cybernetics and Robotics, 2009, Vol. 60, pp. 42 – 54.
7. Zitzler E., Deb K., Thiele L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results // Evolutionary Computation, 2000, Vol. 8(2), pp. 173-195.
8. Карпенко А. П., Селиверстов Е. Ю. Глобальная оптимизация методом роя частиц. Обзор // Информационные технологии, 2010, №2, c. 25-34.
9. Карпенко А. П., Селиверстов Е. Ю. Обзор методов роя частиц для задачи глобальной оптимизации // Наука и образование: электронное научно-техническое издание, 2009, №3. (http://technomag.edu.ru/doc/116072.html).
10. Fonseca C. M., Fleming P. J. Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization / Proc. of the 5th International Conference on Genetic Algorithms, San Mateo, California, 1993, pp. 416-423.
11. Zitzler E., Thiele L., Marco Laumanns M., Fonseca C. M., da Fonseca V. G. Performance Assessment of Multiobjective Optimizers: An Analysis and Review // IEEE Transactions of Evolutionary Computation, 2003, Vol. 7(2), pp. 117-132.
12. Knowles J.D., Corne D.W. On Metrics for Comparing Non-Dominated Sets // Proc. of the 2002 IEEE Congress on Evolutionary Computation (CEC '02), New Jersey, Piscataway, May 2002, IEEE Service Center, 2002, Vol. 1, pp. 711-716.
13. Гуменникова А. В. Адаптивные поисковые алгоритмы для решения сложных задач многокритериальной оптимизации. Диссертация на соискание ученой степени к. т. н.- Красноярск, 2006, 129 с.
14. Luke S. Essentials of Metaheuristics. A Set of Undergraduate Lecture Notes. Department of Computer Science George Mason University, Online Version 1.3 February, 2012. (http://cs.gmu.edu/~sean/book/metaheuristics/Essentials.pdf).
15. Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями: Учебное пособие для ВУЗов.- М.: Дрофа, 2006.- 175 с.
16. Schaffer J.D. Multiple Objective Optimization with Vector Evaluated Genetic Algorithms / In: Genetic Algorithms and Their Applications. Proceedings of the First International Conference on Genetic Algorithms, 1985, Lawrence Erlbaum, pp. 93-100.
17. Моор Д.А., Мухлисуллина Д. Т. Анализ эффективности различных сверток критериев оптимальности в задаче многокритериальной оптимизации // Наука и образование: электронное научно-техническое издание, 2010, №4. (http://technomag.edu.ru/doc/141623.html).
18. Ryu J.-H., Kim S., Wan H. Pareto front approximation with adaptive weighted sum method in multiobjective simulation optimization / Proceedings of the 2009 Winter Simulation Conference (WSC), 2009, Austin, pp. 623-633. (http://www.informs-sim.org/wsc09papers/060.pdf).
19. Srinivas N., Deb K. Multiobjective optimization using nondominated sorting in genetic algorithms // Evolutionary Computation, 1994, vol. 2, p. 221–248.
20. Horn J., Nafpliotis N., Goldberg D.E. A Niched Pareto Genetic Algorithm for Multiobjective Optimization / Proc. of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, New Jersey, 1994, Vol. 1, pp. 82-87.
21. Deb K., Pratap A., Agarwal S., Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II // IEEE Transactions on Evolutionary Computation, 2002, Vol. 6, Issue 2, pp. 182 – 197.
22. Zitzler E., Thiele L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach, IEEE Transactions on Evolutionary Computation, 1999, Vol. 3(4), pp. 257–271.
23. Zitzler E., Laumanns M., Thiele L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm for Multiobjective Optimization / In K.C. Giannakoglou and al., editors. Evolutionary Methods for Design, Optimization and Control with Application to Industrial Problems (EUROGEN 2001), International Center for Numerical Methods in Engineering (CIMNE), 2002, pp. 95‑100.
24. Knowles J., Corne D. The Pareto achieved evolution strategy: A new baseline algorithm for Pareto multiobjective optimization / Proceedings of the Congress on Evolutionary Computation (CEC99), 1999, Washington, Vol. 1, pp. 98–105.
25. Bentley P. J., Wakefield J. P. An Analysis of Multiobjective Optimization within Genetic Algorithms / Technical Report ENGPJB96, University of Huddersfield, UK, 1996. P. 19.
26. Mostaghim S., Teich J. Strategies for Finding Good Local Guides in Multi-objective Particle Swarm Optimization (MOPSO) / In: Swarm Intelligence Symposium, 2003. SIS '03. Proceedingsofthe 2003 IEEE, pp. 26 – 33.
27. Fieldsend J.E., Singh S. A multi-objective algorithm based upon particle swarm optimization, an efficient data structure and turbulence (2002). (http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.19.6959).
28. Coello C.A., Lechuga M.S. MOPSO: A proposal for multiple objective particle swarm optimization / In IEEE Proceedings, World Congress on Evolutionary Computation (CEC2002), 2002, pp. 1051-1056.
29. Hu X., Eberhart R. Multiobjective Optimization Using Dynamic Neighborhood Particle Swarm Optimization / In: Evolutionary Computation, 2002. CEC '02. Proceedings of the 2002 Congress on, Honolulu, HI, USA, 12 – 17 May 2002, pp. 1677 – 1681.
30. Laumanns M., Rudolph G., Schwefel H.P. A spatial predator-prey approach to multi-objective optimization: A preliminary study / In Proceedings of the Parallel Problem Solving from Nature, 1998, Vol. V, pp. 241-249.
31. Deb K. Multi-objective optimization using evolutionary algorithms.- Chichester, UK: Wiley, 2001, P. 518.
32. Deb K., Rao U. B. Investigating Predator-Prey Algorithms for Multi-Objective Optimization / Kanpur Genetic Algorithms Laboratory (KanGAL), Department of Mechanical Engineering Indian Institute of Technology Kanpur, India, KanGAL Report Number 2005010 (http://www.iitk.ac.in/kangal/).
33. Deb K., Mohan M., Mishra S. Evaluating the ![]() -domination based multi-objective evolutionary algorithm for a quick computation of Pareto-optimal solutions // Evolutionary Computation Journal, 2005, Vol. 13(4), pp. 501-525.
-domination based multi-objective evolutionary algorithm for a quick computation of Pareto-optimal solutions // Evolutionary Computation Journal, 2005, Vol. 13(4), pp. 501-525.
34. Антух А.Э., Карпенко А.П., Семенихин А.С., Хасанова Р.В. Построение множества Парето методом роя частиц на графических процессорах архитектуры CUDA // Научный сервис в сети Интернет: суперкомпьютерные центры и задачи: Труды Международной суперкомпьютерной конференции (20-25 сентября 2010 г., г. Новороссийск). М.: Изд-во МГУ, 2010. C. 274-280.
35. Карпенко А.П., Семенихин А.С., Червяцова М.Н. Метод приближенного построения границы области достижимости многосекционного манипулятора типа «хобот» // Наука и образование: электронное научно-техническое издание, 2011, № 1. (http://technomag.edu.ru/doc/165078.html).
Публикации с ключевыми словами: многокритериальная оптимизация, множество Парето, фронт Парето, популяционные алгоритмы
Публикации со словами: многокритериальная оптимизация, множество Парето, фронт Парето, популяционные алгоритмы
Смотри также:
- Модифицированный метод адаптивных взвешенных сумм в задаче многокритериальной оптимизации
- Архитектура и программная реализация системы для оценки качества Парето-аппроксимации в задаче многокритериальной оптимизации
- Распределенная программная система для построения множества Парето в задаче многокритериальной оптимизации динамических систем с использованием параллельного генетического алгоритма
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||